A priority queue is a queue in which we insert an element at the back (enqueue) and remove an element from the front (dequeue). The element with the highest priority shall be dequeued first. This priority queue implementation provides code to implement a priority queue using a heap using iteration, in which the time complexity of enqueue is O(logn), and the space complexity is O(1).
Table of Content
Why use a heap
A heap is a complete binary tree, which is a binary tree in which all levels are completely filled and all the nodes in the last level are as left as possible. Based on this characteristic, it can be represented as an array. Each node’s position in the tree corresponds to the index in the array as following diagram.
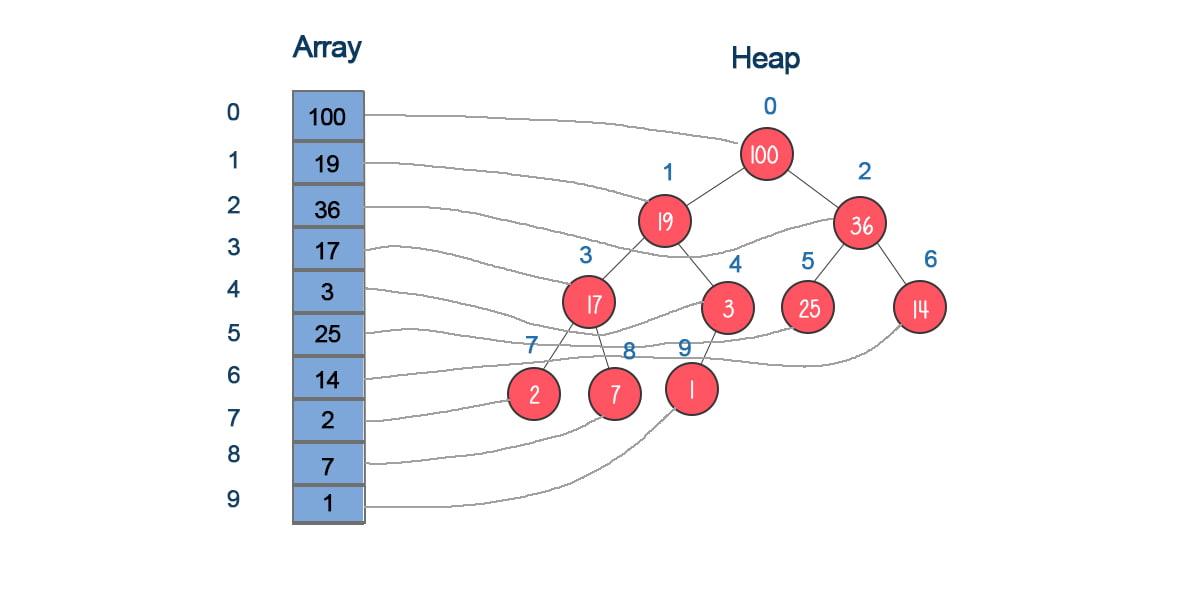
You can get the parent or children’s indices by the current index:
parentIndex = (index-1) / 2
leftIndex = 2*index + 1
rightIndex=2*index + 2
Meanwhile, a heap should also meet this criterion: the parent’s value is larger than both children’s values. The max value is stored in the root. So a heap is partially sorted. Based on this, you can use a heap to implement a priority queue.
Please note when you use max heap, the priority queue is a descending priority queue (ie the bigger the key, the higher the priority). If you use min heap to implement. the priority queue is an ascending priority queue.
Map of priority queue implementations
Part 1 – priority queue implementation with an unordered array
Part 2 – priority queue implementation with an ordered array
Part 3 – priority queue implementation with heap – iterative solution
Part 4 – priority queue implementation with heap – recursive solution
Enqueue
In the class, declare three attributes: heap, length, and maxSize. heap is an array. maxSize is the max length of the array. It is used to initialize the array. length is the actual number of elements in the array. It starts from 0.
To enqueue, you put the new value at the end of the array. Then move it up based on its value compared to its parent. If its value is larger than its parent, it should be switched to the position with its parent. We call this process bubble up or heap up. The time complexity is O(logn).
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
//Descending priority, the higher the value, the higher the priority public class PriorityQueueHeapIterative<T extends Comparable<T>> { T[] heap; int length; int maxSize; //Time O(1) Space O(1) @SuppressWarnings("unchecked") public PriorityQueueHeapIterative(int capacity) { maxSize = capacity; heap = (T[]) new Comparable[capacity]; length = 0; // means queue is empty } //Insert a new value in max heap, Time O(logn), Space O(1), public void enqueue(T value) { if (length == maxSize) { System.out.println("priority queue is full, cannot enqueue " + value); return; } heap[length] = value; heapUp(length); //start from last length++; } //Time O(logn), Space O(1) private void heapUp(int pos) { int parentPos = (pos-1)/2; T value = heap[pos]; while (pos > 0 && (value.compareTo(heap[parentPos]) > 0)) { heap[pos] = heap[parentPos]; pos = parentPos; parentPos = (parentPos-1)/2; } heap[pos] = value; } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
//Descending priority, the higher the key, the higher the priority class PriorityQueueHeapIterative { //Time O(1) Space O(1) constructor (capacity) { this.maxSize = capacity; this.length = 0; this.heap = []; } //Insert a new value in max heap, Time O(logn), Space O(1), n is number of items in heap enqueue(value) { if (this.length >= this.maxSize) { console.log("priority queue is full, cannot enqueue "); return; } this.heap[this.length] = value; this.heapUp(this.length); this.length++; } //Time O(logn), Space O(1) heapUp(pos) { var parentPos = Math.floor((pos-1)/2); var value = this.heap[pos]; while (pos > 0 && value > this.heap[parentPos]) { this.heap[pos] = this.heap[parentPos]; pos = parentPos; parentPos= Math.floor((parentPos-1)/2); } this.heap[pos] = value; } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# Descending priority, the higher the value, the higher the priority class PriorityQueueHeapIterative: # Time O(1) Space O(1) def __init__(self, capacity): self.maxSize = capacity self.length = 0 self.heap = [None]*capacity # Insert a new value in max heap, Time O(logn), Space O(1) def enqueue(self, value): if self.length >= self.maxSize: print("priority queue is full, cannot enqueue") return self.heap[self.length] = value # start from last self.heapUp(self.length) self.length += 1 # Time O(logn), Space O(1) def heapUp(self, pos): parentPos = int((pos-1)/2) value = self.heap[pos] while pos > 0 and value > self.heap[parentPos]: self.heap[pos] = self.heap[parentPos] pos = parentPos parentPos= int((parentPos-1)/2) self.heap[pos] = value |
Doodle
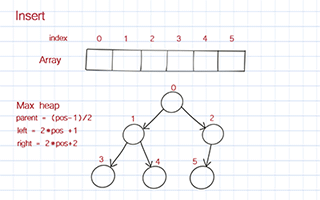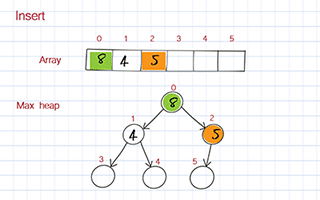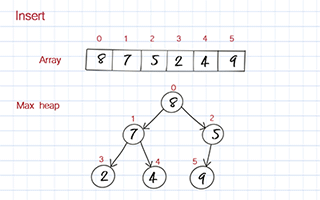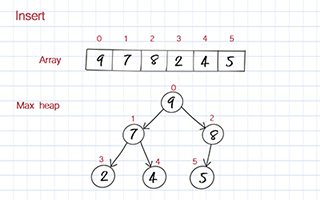
Dequeue
The dequeue operation is to remove the highest priority element, which is the first one in the array. When you remove the first element in the array, you move the last element to the first position to fill out the empty spot. But this element’s value might be smaller than its children. To correct this, you compare its value with its children’s values and switch with the child with the larger value. This process is called bubble down or heap down. The time complexity is O(logn).
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
//Remove from max (first one), Time O(logn), Space O(1), no recursion public T dequeue() { if (length == 0) { System.out.println("queue is empty"); return null; } T max = heap[0]; heap[0] = heap[length-1]; //last put first length--; heapDown(0); return max; } //Time O(logn), space O(1) private void heapDown(int pos) { T item = heap[pos]; int index; while (pos < length/2) { int left = 2*pos + 1; int right = 2*pos + 2; if (right < length && heap[left].compareTo(heap[right]) < 0) index = right; else index = left; if (item.compareTo(heap[index]) >= 0) break; heap[pos] = heap[index]; pos = index; } heap[pos] = item; } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
//Remove from max (first one), Time O(logn), Space O(1) dequeue() { if (this.length == 0) { console.log("queue is empty"); return null; } var max = this.heap[0]; this.heap[0] = this.heap[this.length-1];//put last at first this.length--; this.heapDown(0); return max; } //Time O(logn), space O(1) heapDown(pos) { var item = this.heap[pos]; var index; while (pos < Math.floor(this.length/2)) { let left = 2*pos + 1; let right = 2*pos + 2; if (right < this.length && this.heap[left] < this.heap[right]) index = right; else index = left; if (item >= this.heap[index]) break; this.heap[pos] = this.heap[index]; pos = index; } this.heap[pos] = item; } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# Remove from max (first one), Time O(logn), Space O(1), no recursion def dequeue(self): if self.length == 0: print("queue is empty") return None max = self.heap[0] self.heap[0] = self.heap[self.length-1] # put last at first self.length -= 1 self.heapDown(0) return max # Time O(logn), Space O(1) def heapDown(self, pos): item = self.heap[pos] index = 0 while pos < int(self.length/2): left = 2*pos + 1 right = 2*pos + 2 if right < self.length and self.heap[left] < self.heap[right]: index = right else: index = left if item >= self.heap[index]: break self.heap[pos] = self.heap[index] pos = index self.heap[pos] = item |
Doodle
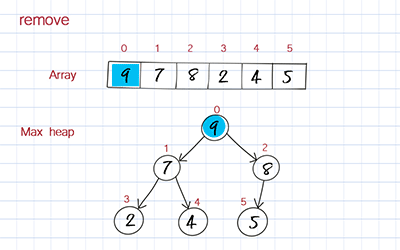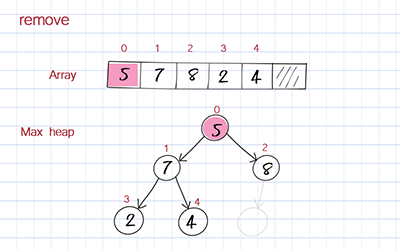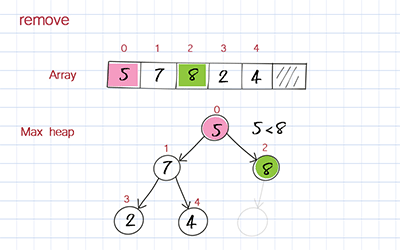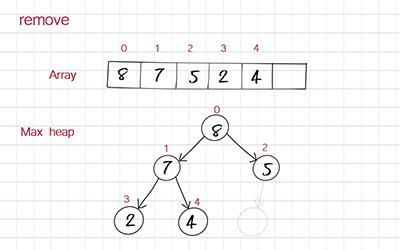
Peek
Peek is to return the value of the highest priority element. Since the first one already has the largest value, this can be done by returning the first element in the array.
Java
|
1 2 3 4 5 6 7 8 |
//Time O(1) Space O(1) public T peek() { if (length == 0) { System.out.println("queue is empty"); return null; } return heap[0]; } |
Javascript
|
1 2 3 4 5 6 7 8 |
//Time O(1) Space O(1) peek() { if (this.length == 0) { console.log("queue is empty"); return null; } return this.heap[0]; } |
Python
|
1 2 3 4 5 6 |
#Time O(1) Space O(1) def peek(self): if self.length == 0: print("queue is empty") return None return self.heap[0] |
Print
Print is to print all elements in the array, starting from the index 0 to the highest index. A for loop is used to iterate through each element.
Java
|
1 2 3 4 5 6 |
//Print as array, Time O(n), Space O(1) public void print() { for (int i = 0; i < length; i++) System.out.print(heap[i] + " "); System.out.println(); } |
Javascript
|
1 2 3 4 5 6 7 8 |
//Print as array, Time O(n), Space O(n) print() { var s = ""; for (let i = 0; i < this.length; i++) { s += this.heap[i] + " " ; } console.log(s); } |
Python
|
1 2 3 4 5 |
#Print as array, Time O(n), Space O(1) def print(self): for i in range( 0, self.length, +1): print(self.heap[i], end = ' ') print() |
Free download
Download priority queue using heap (iterative solution) in Java, JavaScript and Python
Data structures introduction PDF
What are the ways to implement a priority queue using a heap?
There are two ways to implement a priority queue with a heap: iteration and recursion. Their time complexities are the same O(logn). But recursion needs memory space for function calls’ call stacks, while iteration doesn’t. So iterative method is better.