A priority queue is a queue in which we insert an element at the back (enqueue) and remove an element from the front (dequeue). The element with the highest priority shall be dequeued first. The Priority queue can be implemented with array or heap.
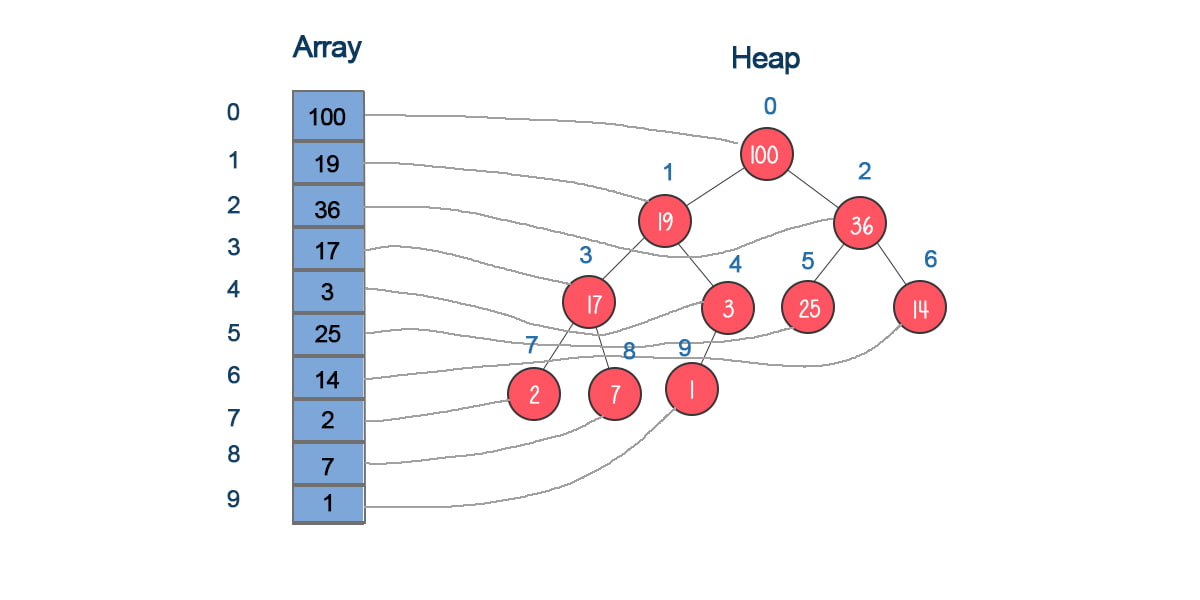
We have introduced why we use heap to implement priority queue.
Table of Content
Map of priority queue implementations
Part 1 – priority queue implementation with ordered array
Part 2 – priority queue implementation with unordered array
Part 3 – priority queue implementation with heap – iterative solution
Part 4 – priority queue implementation with heap – recursive solution
Enqueue
First we declare three attributes: heap, length and maxSize. heap is an array to hold all elements in the priority queue. maxSize is the max size of the array. length is actual number of elements in the array. It starts from 0.
To enqueue, we put the new value at the end of the array. Then we move it up based on its value compared to its parent. If it’s value larger than its parent, it should be swapped with its parent. We call this process bubble up or heap up. The time complexity is O(logn).
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
public class PriorityQueueHeap2<T extends Comparable<T>> { T[] heap; int length; int maxSize; //Constructor, Time O(1) Space O(1) @SuppressWarnings("unchecked") public PriorityQueueHeap2(int capacity) { maxSize = capacity; length = 0; heap = (T[]) new Comparable[maxSize]; } //Insert a new value in max heap, Time O(h), Space O(1), n is number of items in heap //h is height of heap (complete binary tree) h = log(n) public void enqueue(T value) { if (length == maxSize) { System.out.println("priority queue is full, cannot enqueue " + value); return; } heap[length] = value; heapUp(length++); } //Time O(h), Space O(1), use swap private void heapUp(int pos) { while (heap[pos].compareTo(heap[(pos-1)/2]) > 0) { swap(pos, (pos-1)/2); pos = (pos-1)/2; } } //Time O(1) Space O(1) private void swap(int p1, int p2) { T tmp = heap[p1]; heap[p1] = heap[p2]; heap[p2] = tmp; } } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
class PriorityQueueHeap2 { //Constructor, Time O(1) Space O(1) constructor(capacity) { this.maxSize = capacity; this.length = 0; this.heap = {}; } //Insert a new value in max heap, Time O(h), Space O(1), n is number of items in heap //h is height of heap (complete binary tree) h = log(n) enqueue(value) { if (this.length == this.maxSize) { console.log("priority queue is full, cannot enqueue " + value); return; } this.heap[this.length] = value; this.heapUp(this.length++); } //Time O(h), Space O(1), use swap heapUp(pos) { while (this.heap[pos] > this.heap[Math.floor((pos-1)/2)] ) { this.swap(pos, Math.floor((pos-1)/2)); pos = Math.floor((pos-1)/2); } } //Time O(1) Space O(1) swap (p1, p2) { var tmp = this.heap[p1]; this.heap[p1] = this.heap[p2]; this.heap[p2] = tmp; } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
class PriorityQueueHeap2 : # Time O(1) Space O(1) def __init__(self, capacity) : self.maxSize = capacity self.length = 0 self.heap = [None]*capacity #Insert a new value in max heap, Time O(h), Space O(1), n is number of items in heap # h is height of heap (complete binary tree) h = log(n) def enqueue(self, value): if self.length >= self.maxSize : print("reach max size, return") return self.heap[self.length] = value # put at last first self.heapUp(self.length) # Time O(h), Space O(1), use swap def heapUp(self, pos): while self.heap[pos] > self.heap[int((pos-1)/2)] : self.swap(pos, int((pos-1)/2)) pos = int((pos-1)/2) self.length +=1 # Time O(1) Space O(1) def swap (self, p1, p2) : tmp = self.heap[p1] self.heap[p1] = self.heap[p2] self.heap[p2] = tmp |
Doodle
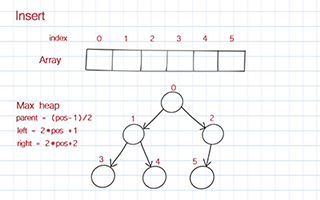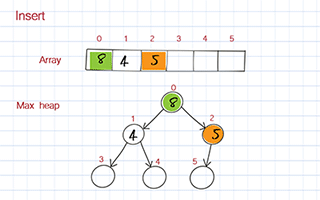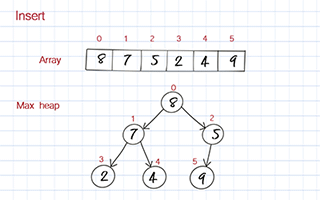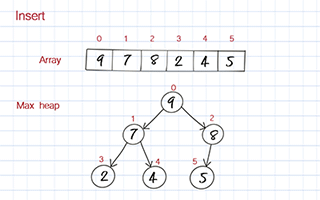
Dequeue
The dequeue operation is to remove the highest priority element from the array. When we remove the first element in the array, we move the last element to fill out the empty spot. But this element’s value might be smaller than its children’s. To correct this, we compare its value with its children’s values, and switch with the child with the larger value. This process is called bubble down or heap down.
Please note this implementation is using recursion. The time complexity is the same as iterative implementation O(logn). However, the space complexity has increased to O(logn) for the call stack. So it is not as efficient as iterative approach.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
//Remove from max (first one), Time O(h), Space O(h), call recursion public T dequeue() { if (length == 0) { System.out.println("queue is empty"); return null; } T max = heap[0]; heap[0] = heap[length-1]; //last put at first length--; heapDown(0); return max; } //Use recursion, Time O(h), Space O(h) private void heapDown(int pos) { if (pos >= (length / 2) && pos <= length) //reach leaf return; if (heap[pos].compareTo(heap[2*pos+1]) < 0 || heap[pos].compareTo(heap[2*pos+2]) < 0) { if (heap[2*pos+1].compareTo(heap[2*pos+2]) >0) { swap(pos, 2*pos+1); heapDown(2*pos+1); } else { swap(pos, 2*pos+2); heapDown(2*pos+2); } } } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
//Remove from max (first one), Time O(h), Space O(h), call recursion dequeue() { if (this.length == 0) { console.log("queue is empty"); return null; } var max = this.heap[0]; this.heap[0] = this.heap[this.length-1]; //put last at first this.length--; this.heapDown(0); return max; } //Recursion, Time O(h), Space O(h) heapDown(pos) { if (pos >= Math.floor(this.length/2) && pos <= this.length) //reach leaf return; if (this.heap[pos] < this.heap[2*pos+1] || this.heap[pos] < this.heap[2*pos+2]) { if (this.heap[2*pos+1] > this.heap[2*pos+2]) { this.swap(pos, 2*pos+1); this.heapDown(2*pos+1); } else { this.swap(pos, 2*pos+2); this.heapDown(2*pos+2); } } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# Remove from max (first one), Time O(h), Space O(h), call recursion def dequeue(self) : max = self.heap[0] self.heap[0] = self.heap[self.length-1] #put the last at first self.length -= 1 self.heapDown(0) return max # Use recursion, Time O(h), Space O(h) def heapDown(self, pos) : if pos >= int(self.length/2) and pos <= self.length : #reach leaf return; if self.heap[pos] < self.heap[2*pos+1] or self.heap[pos] < self.heap[2*pos+2] : if self.heap[2*pos+1] > self.heap[2*pos+2] : self.swap(pos, 2*pos+1) self.heapDown(2*pos+1) else : self.swap(pos, 2*pos+2) self.heapDown(2*pos+2) |
Doodle
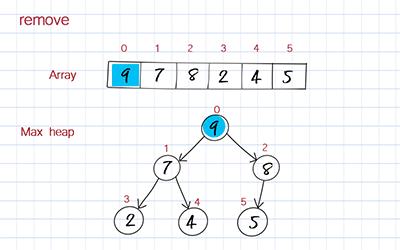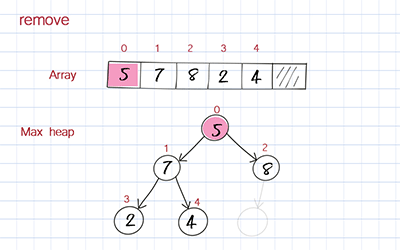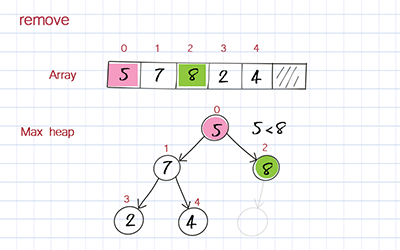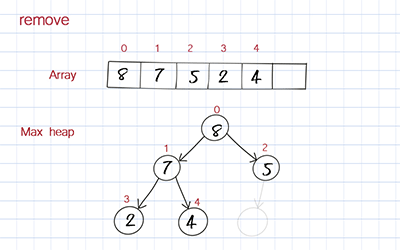
Peek
Peek is to return the value of the highest priority element. Since the first one already has the largest value, this can be done by returning the first element in the array.
Java
|
1 2 3 4 |
//Time O(1) Space O(1) public T peek() { return heap[0]; } |
Javascript
|
1 2 3 4 |
//Time O(1) Space O(1) peek() { return this.heap[0]; } |
Python
|
1 2 3 |
# Time O(1) Space O(1) def peek(self): return self.heap[0] |
Print
Print is to print all elements in the array, starting from the index 0 to highest index. A for loop is used to iterate through each element.
Java
|
1 2 3 4 5 6 7 |
//Print as array, Time O(n), Space O(1) public void print() { System.out.print("Priority Queue: "); for (int i = 0; i < length; i++) System.out.print(heap[i] + " "); System.out.println(); } |
Javascript
|
1 2 3 4 5 6 7 8 |
//Print as array, Time O(n), Space O(1) print() { var s = ""; for(let i = 0; i < this.length; i++) { s += this.heap[i] + " " ; } console.log(s); } |
Python
|
1 2 3 4 5 6 |
#Print as array, Time O(n), Space O(1) def print(self) : s = [] for i in range(0, self.length): s.append(self.heap[i]) print(s) |
Free download
Download priority queue implementation using heap (recursive) in Java, JavaScript and Python
Data structures introduction PDF
What data structures are used to implement a priority queue?
An array or a heap can be used to implement a priority queue. When using an array, the time complexity of enqueue or dequeue is O(n). When using a heap, the time complexity is O(logn). So heap is better.