The Fibonacci Sequence is the series of numbers: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 … The next number is found by adding up the two numbers before it. In this post, we are going to find n-th Fibonacci number for any given number n. There are 4 implementations. They are iteration, dynamic programming, recursion, and memoization.
Table of content
- 1. Iterative solution
- 2. Dynamic programming solution
- 3. Recursive solution
- 4. Memoization solution
- Download and FAQ
1. Iterative solution
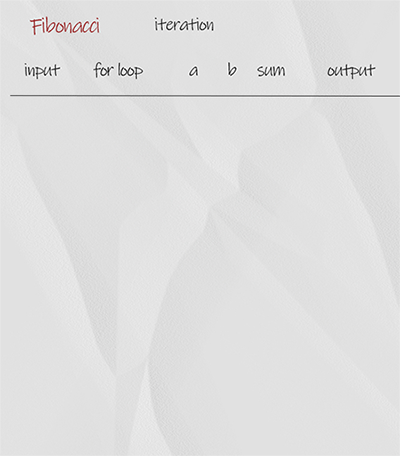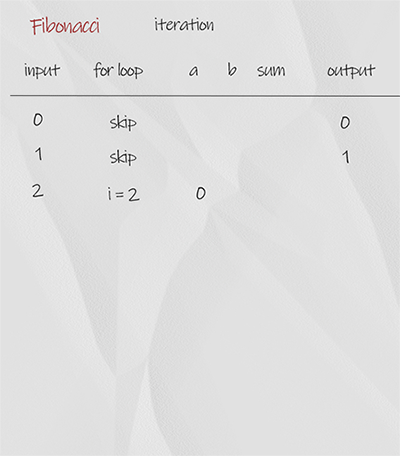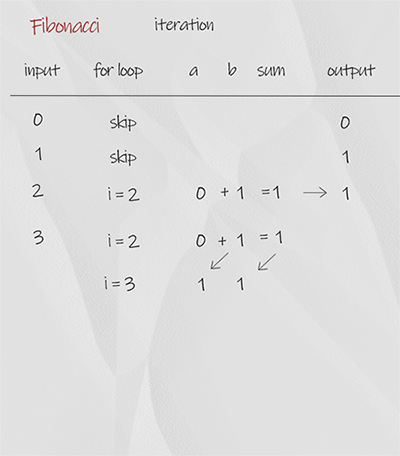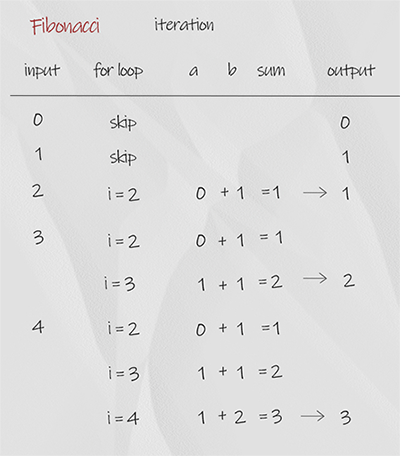
We use for loop starting from 2. In each iteration, variable sum in the sum of previous two number a and b. When finish, return sum. The time complexity is O(n), space complexity is O(1). It is the best solution.
Java
1 2 3 4 5 6 7 8 9 10 11 12 | //Iteration, Time O(n), Space space O(1), n is input number public static int fibonacci(int n) { if (n <=1) return n; int a = 0, b = 1, sum = 1; for (int i = 2; i <= n; i++) { sum = a + b; a = b; b = sum; } return sum; } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 | //Iteration, Time O(n), Space space O(1), n is input number function fibonacci(num) { if (num <= 1) return num; var a = 0, b = 1, sum = 1; for (let i = 2; i <= num; i++) { sum = a + b; a = b; b = sum; } return sum; } |
Python
1 2 3 4 5 6 7 8 9 10 11 | #Iteration, Time O(n), Space space O(1), n is input number def fibonacci(num) : if num <= 1: return num a = 0 b = 1 for i in range(2, num+1): sum = a + b a = b b = sum return sum |
Doodle
2. Dynamic programming solution
The basic idea is the same as iteration. In additional, we use an array to save all the result. At the end we return the value with the index of the input number from the array. The time complexity is O(n), space complexity is O(n).
Java
1 2 3 4 5 6 7 8 9 10 11 | //Dynamic programming, Time O(n), Space O(n) public static int fibonacciDP(int n) { if (n <= 1) return n; int[] dp = new int[n+1]; dp[1] = 1; for (int i = 2; i <= n; i++) { dp[i] = dp[i-1] + dp[i-2]; } return dp[n]; } |
Javascript
1 2 3 4 5 6 7 8 9 10 | //Dynamic programming, time O(n), Space O(n) function fibonacciDP(n){ let dp = {}; //itialize the memo dp[0] = 0; dp[1] = 1; for (let i = 2; i <= n; i++){ dp[i] = dp[i-1] + dp[i-2]; } return dp[n]; } |
Python
1 2 3 4 5 6 | #Dynamic programming, time O(n), Space O(n) def fibonacciDP(n): dp = [0, 1] # initialize the first two fibonacci numb for i in range(2, n+1): dp.append(dp[i-1] + dp[i-2]) return dp[n] |
Doodle

3. Recursive solution
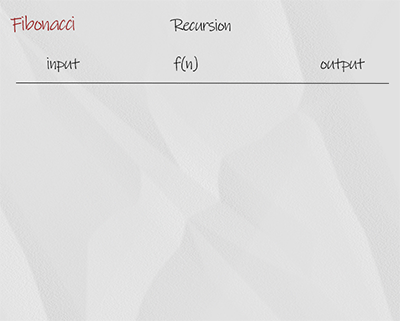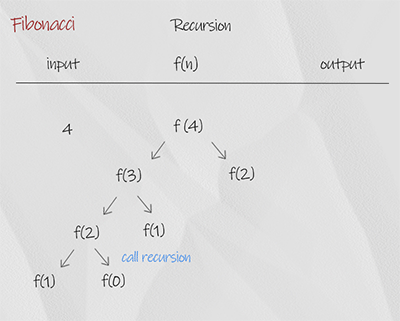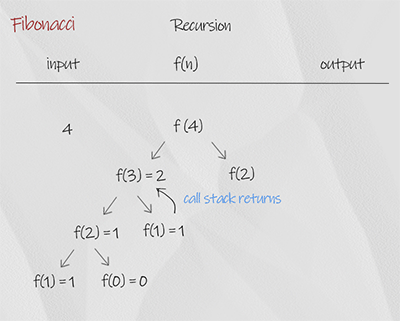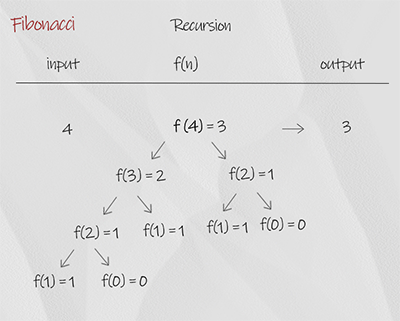
The recursion is a simple implementation of the concept, in which each number is the sum of the previous of two number. The base condition is when input is 0 or 1, it return the number itself. It is not efficient. For example, when the input is 4, it calls f(2) twice. So there is overlapping. The time complexity is O(2^n), space complexity is O(n). It is the worst solution.
Java
1 2 3 4 5 6 | //Recursion, Time O(2^n), Space O(n) public static int fibonacciRec(int n) { if (n <= 1) return n; return fibonacciRec(n-1) + fibonacciRec(n-2); } |
Javascript
1 2 3 4 5 6 | //Recursion, Time O(2^n), Space O(n) function fibonacciRec(num) { if (num <= 1) return num; return fibonacciRec(num-1) + fibonacciRec(num-2); } |
Python
1 2 3 4 5 | #Recursion, Time O(2^n), Space O(n) def fibonacciRec(num) : if num <= 1: return num return fibonacciRec(num-1) + fibonacciRec(num-2) |
Doodle
4. Memoization solution
This method is to overcome the overlapping in recursion using memoization. The solution uses an array to store the partial result. For example, if the result of f(2) is saved, next time the function finds the result in array and returns it. Memoization is one of techniques in called dynamic programming. The time complexity is O(n), space complexity is O(n).
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 | //Recursion + memoization(DP), Time O(n), Space O(n) public static int fibonacciRecMemo(int n) { int[] memo = new int[n+1]; return fibHelper(n, memo); } private static int fibHelper(int n, int[] memo) { if (memo[n] != 0) return memo[n]; if (n <= 1) return n; return memo[n] = fibHelper(n-1, memo) + fibHelper(n-2, memo); } |
Javascript
1 2 3 4 5 6 7 8 9 | //Recursion + memoization(DP), Time O(n), Space O(n) function fibonacciRecMemo(n, memo) { memo = memo || {}; //if no memo, intialize {}, else get values from memo if (n <= 1) return n; if (memo[n]) //check memoization return memo[n]; return memo[n] = fibonacciRecMemo(n-1, memo) + fibonacciRecMemo(n-2, memo); } |
Python
1 2 3 4 5 6 7 8 9 10 11 | memo = [] for i in range(num+1): memo.append(0) #Recursion + memoization(DP), Time O(n), Space O(n) def fibonacciRecMemo(n): if n <= 1: return n if memo[n] != 0: return memo[n] memo[n] = fibonacciRecMemo(n-1) + fibonacciRecMemo(n-2) return memo[n] |
Doodle

Download
Download source code in Java, JavaScript and Python
View animation how Fibonacci recursion works
View animation how Fibonacci memoization works
Numbers and recursions doodle compilation(YouTube)
What are the 4 solutions to find the nth Fibonacci number?
From best to worst:
1. Iterative solution, O(n) time, O(1) space.
2. Dynamic programming using an extra array: O(n) time, O(n) space.
3. Dynamic programming using Memoization, O(n) time, O(n) space.
4. Recursion, O(2^n) time, O(n) space.