A max-heap is a complete binary tree, where all levels, except the last level, are completely filled. There is no “hole” in the tree. A max-heap should also meet these criteria: the parent’s value is larger than both children’s values in a sub-tree. The largest value of the heap is at the root. The heap is usually related to the priority queue and heapsort.
This post is the max heap implementation. The min-heap is in the opposite order.
Table of Content
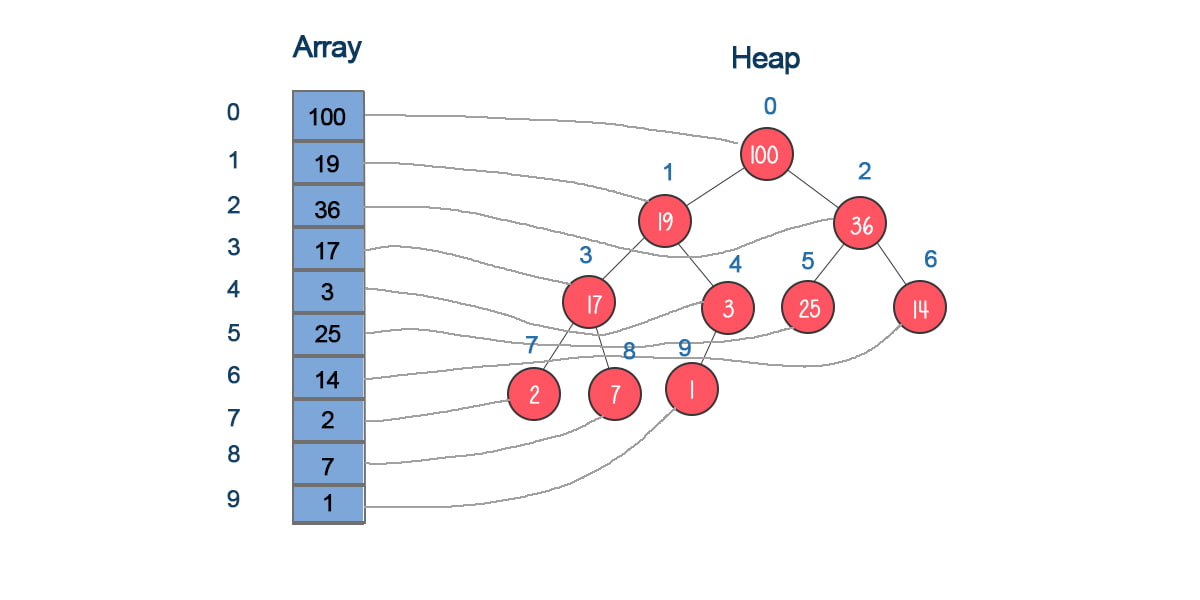
What data structure is underneath of heap implementation?
A heap is a complete binary tree conceptually. The underlying data structure is an array. Each node’s position in the heap is corresponding to the index in the array. The root’s position is 0, corresponding to the index 0. The node’s position increases by 1 from left to right, from top to bottom.
What is the formula to get the parent and two children’s positions from the current node’s position in a heap?
parentPos = (pos-1)/2
left = 2*pos+1
right=2*pos+2
What is the bubble-up algorithm in the heap?
To insert a new element in a heap, the algorithm bubble up is used. It is to put the new item in the first vacant cell of the array. Then move it up in the heap based on its value compared to its parent. In a max-heap, it should be below a node with a larger value and above one or two child nodes with smaller values.
What is the bubble-down algorithm in the heap?
Bubble-down is an algorithm used in heap deletion. It is to compare the parent node with child nodes in a subtree. In a max-heap, if the parent node’s value is smaller, you should switch the parent element with a child node that has a larger value.
What is max heap?
A max-heap is a complete binary tree, where all levels, except the last level, are completely filled. There is no “hole” in the tree. A max-heap should also meet these criteria: the parent’s value is larger than both children’s values. The largest value is at the root.
Map of heap implementations
Part 1 – Max-heap implementation
Part 2 – Min-heap implementation
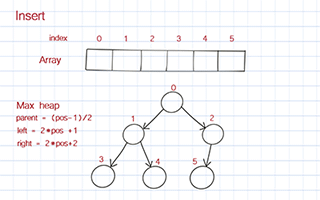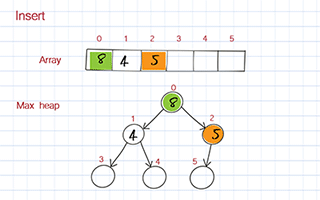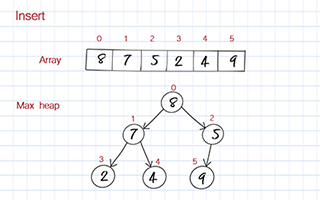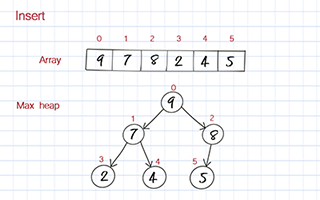
Insert
We declare three attributes: heap, length, and maxSize. heap is an array. maxSize is the max length of the array. It is used to initialize the array. length is the actual number of elements in the array. It starts from 0.
To insert a new element, we put the new value at the end of the array. Then we move it up in the heap based on its value compared to its parent. If its value is larger than its parent, it should be switched the position with its parent. We keep doing it until it is below a node with a larger value and above one or two nodes with smaller values. We call this process bubble up.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | import java.util.*; public class MaxHeap<T extends Comparable<T>> { T[] heap; int length; int maxSize; //Time O(1) Space O(1) @SuppressWarnings("unchecked") public MaxHeap(int capacity) { maxSize = capacity; heap = (T[]) new Comparable[capacity]; length = 0; // means queue is empty } //Insert a new value, Time O(logn), Space O(1), n is number of items in heap public void insert(T value) { if (length == maxSize) { System.out.println("heap is full, cannot insert " + value); return; } heap[length]= value; bubbleUp(length); length++; } //Time O(logn), Space O(1) private void bubbleUp(int pos) { int parentPos = (pos-1)/2; T value = heap[pos]; while (pos > 0 && (value.compareTo(heap[parentPos]) > 0)) { heap[pos] = heap[parentPos]; pos = parentPos; parentPos= (parentPos-1)/2; } heap[pos] = value; } } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | class MaxHeap { //Constructor, Time O(1) Space O(1) constructor(capacity) { this.maxSize = capacity; this.length = 0; this.heap = []; } //Insert a new value, Time O(logn), Space O(1), n is number of items in heap insert(value) { if (this.length >= this.maxSize) { console.log("heap is full, cannot insert"); return; } this.heap[this.length] = value; this.bubbleUp(this.length); this.length++; } //Time O(logn), Space O(1) bubbleUp(pos) { var parentPos = Math.floor((pos-1)/2); var value = this.heap[pos]; while (pos > 0 && value > this.heap[parentPos]) { this.heap[pos] = this.heap[parentPos]; pos = parentPos; parentPos= Math.floor((parentPos-1)/2); } this.heap[pos] = value; } } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | class MaxHeap: #Time O(1) Space O(1) def __init__(self, capacity): self.maxSize = capacity self.length = 0 self.heap = [None]*capacity #Insert a new value, Time O(logn), Space O(1), n is number of items in heap def insert(self, value): if self.length >= self.maxSize: print("heap reach max size, return") return self.heap[self.length] = value # start from last self.bubble_up(self.length) self.length += 1 #Time O(logn), Space O(1) def bubble_up(self, pos): parentPos = int((pos-1)/2) value = self.heap[pos] while pos > 0 and value > self.heap[parentPos]: self.heap[pos] = self.heap[parentPos] pos = parentPos parentPos = int((parentPos-1)/2) self.heap[pos] = value |
Doodle
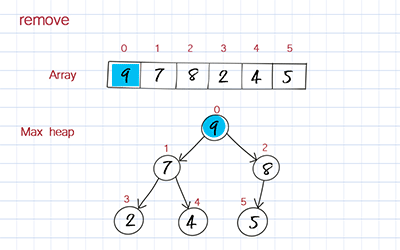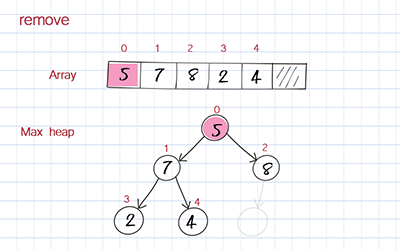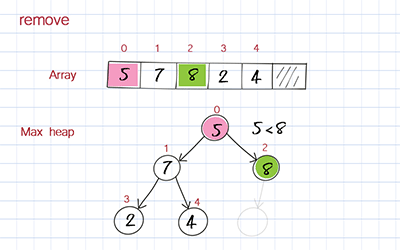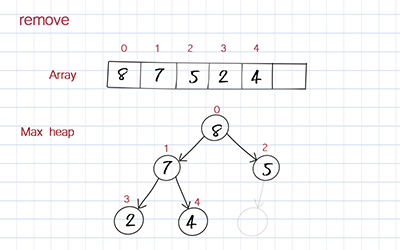
Remove
The removal operation is to remove the element at the root, which has the highest value. This is the first element in the underlying array. When we remove the first element in the array, we move the last element to fill out the empty spot. But this element’s value might be smaller than its children’s. To correct this, we compare its value with its children’s values and switch with the child with the larger value. We keep doing it until it is below a node with a larger value and above one or two nodes with smaller values. This process is called bubble down. Bubble down is more complicated than bubble up because it has two children to compare.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | //Remove from max (first one), Time O(logn), Space O(1) public T remove() { if (length == 0) { System.out.println("heap is empty"); return null; } T max = heap[0]; heap[0] = heap[length-1]; //put last at first length--; bubbleDown(0); return max; } //Time O(logn), space O(1) private void bubbleDown(int pos) { T item = heap[pos]; int index; while (pos < length/2) { int left = 2*pos + 1; int right = 2*pos + 2; if (right < length && heap[left].compareTo(heap[right]) < 0) index = right; else index = left; if (item.compareTo(heap[index]) >= 0) break; heap[pos] = heap[index]; pos = index; } heap[pos] = item; } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | //Remove from max (first one), Time O(logn), Space O(1) remove() { if (this.length == 0) { console.log("heap is empty"); return null; } var max = this.heap[0]; this.heap[0] = this.heap[this.length-1];//put last to first this.length--; //reduce length this.bubbleDown(0); return max; } //Time O(logn), Space O(1) bubbleDown(pos) { var item = this.heap[pos]; var index; while (pos < Math.floor(this.length/2)) { let left = 2*pos + 1; let right = 2*pos + 2; if (right < this.length && this.heap[left] < this.heap[right]) index = right; else index = left; if (item >= this.heap[index]) break; this.heap[pos] = this.heap[index]; pos = index; } this.heap[pos] = item; } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | #Remove from max (first one), Time O(logn), Space O(1) def remove(self): if self.length == 0: print("heap is empty") return None max = self.heap[0] self.heap[0] = self.heap[self.length-1] # put last at first self.length -= 1 self.bubble_down(0) return max # Time O(logn), Space O(1) def bubble_down(self, pos): item = self.heap[pos] index = 0 while pos < int(self.length/2): left = 2*pos + 1 right = 2*pos + 2 if right < self.length and self.heap[left] < self.heap[right]: index = right else: index = left if item >= self.heap[index]: break self.heap[pos] = self.heap[index] pos = index self.heap[pos] = item |
Doodle
Search
Since the underlying data structure is an array, we iterate through all elements to find the one that matches the key.
Java
1 2 3 4 5 6 7 8 | //Time O(n), Space O(1), n is number of items in heap public boolean search(T key) { for (int i = 0; i < length; i++) { if (key.compareTo(heap[i]) == 0) return true; } return false; } |
Javascript
1 2 3 4 5 6 7 8 | //Time O(n), Space O(1), n is number of items in heap search(key) { for (let i = 0; i < this.length; i++) { if (key == this.heap[i]) return true; } return false; } |
Python
1 2 3 4 5 6 | #Time O(n), Space O(1), n is number of items in heap def search(self, key): for i in range(0, self.length): if key == self.heap[i]: return True return False |
Traversal
The traversal operation is to visit all nodes in the tree. This is the same as a traversal in a binary tree. There are four ways: level order, preorder, inorder, and postorder.
Level order is to visit nodes level by level from top to bottom. The order is the same as the visiting array from index 0 to its length.
Java
1 2 3 4 5 6 7 8 | //Traverse as array, it is also level order of tree, Time O(n), Space O(n) public List<T> levelOrder() { List<T> list = new ArrayList<>(); for(int i = 0; i < length; i++) { list.add(heap[i]); } return list; } |
Javascript
1 2 3 4 5 6 7 8 | //Traverse as array, it is also level order of tree, Time O(n), Space O(n) levelOrder() { var str = []; for(let i = 0; i < this.length; i++) { str.push(this.heap[i]); } return str; } |
Python
1 2 3 4 5 6 | # Traverse as array, it is also level order of tree, Time O(n), Space O(n) def levelOrder(self): s = [] for i in range(0, self.length): s.append(self.heap[i]) return s |
The preorder traversal is to visit the root, traverse the left subtree, and traverse the right subtree. The implementation uses DFS recursion. To get the children’s positions, we use the formula 2*pos+1 for the left child, and 2*pos+2 for the right child.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | //Traverse as tree preorder, Time O(n), Space O(n) public List<T> preorder() { List<T> list = new ArrayList<>(); preorderRec(0, list); return list; } //Recursion helper, Time O(n), Space O(n) private void preorderRec(int nodeIndex, List<T> list) { if (nodeIndex > length-1) return; list.add(heap[nodeIndex]); preorderRec(2*nodeIndex + 1, list); preorderRec(2*nodeIndex + 2, list); } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | //Traverse as tree preorder, Time O(n), Space O(n) preorder() { var output = []; this.preorderRec(0, output); return output; } //Recursion helper, Time O(n), Space O(n) preorderRec(nodeIndex, output) { if (nodeIndex > this.length-1) return; output.push(this.heap[nodeIndex]); this.preorderRec(2*nodeIndex + 1, output); this.preorderRec(2*nodeIndex + 2, output); } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 | # Traverse as tree preorder, Time O(n), Space O(n) def preorder(self): output = [] self.preorderRec(0, output) return output # Recursion helper, Time O(n), Space O(n) def preorderRec(self, nodeIndex, output): if nodeIndex > self.length-1: return output.append(self.heap[nodeIndex]) self.preorderRec(2*nodeIndex + 1, output) self.preorderRec(2*nodeIndex + 2, output) |
The inorder traversal is to traverse the left subtree, visit the root, and traverse the right subtree. The implementation uses DFS recursion. To get the children’s positions, we use the formula 2*pos+1 for the left child, and 2*pos+2 for the right child.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | //Traverse as tree inorder, Time O(n), Space O(n) public List<T> inorder() { List<T> list = new ArrayList<>(); inorderRec(0, list); return list; } //Recursion helper, Time O(n), Space O(n) private void inorderRec(int nodeIndex, List<T> list) { if (nodeIndex > length-1) return; inorderRec(2*nodeIndex + 1, list); list.add(heap[nodeIndex]); inorderRec(2*nodeIndex + 2, list); } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | //Traverse as tree inorder, Time O(n), Space O(n) inorder() { var output = []; this.inorderRec(0, output); return output; } //Recursion helper, Time O(n), Space O(n) inorderRec(nodeIndex, output) { if (nodeIndex > this.length-1) return; this.inorderRec(2*nodeIndex + 1, output); output.push(this.heap[nodeIndex]); this.inorderRec(2*nodeIndex + 2, output); } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 | # Traverse as tree inorder, Time O(n), Space O(n) def inorder(self): output = [] self.inorderRec(0, output) return output # Recursion helper, Time O(n), Space O(n) def inorderRec(self, nodeIndex, output): if nodeIndex > self.length-1: return self.inorderRec(2* nodeIndex + 1, output) output.append(self.heap[nodeIndex]) self.inorderRec(2*nodeIndex + 2, output) |
The postorder traversal is to traverse the left subtree, traverse the right subtree, and visit the root. The implementation uses DFS recursion. To get the children’s positions, we use the formula 2*pos+1 for the left child, and 2*pos+2 for the right child.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | //Traverse as tree postorder, Time O(n), Space O(n) public List<T> postorder() { List<T> list = new ArrayList<>(); postorderRec(0, list); return list; } //Recursion helper, Time O(n), Space O(n) private void postorderRec(int nodeIndex, List<T> list) { if (nodeIndex > length-1) return; postorderRec(2*nodeIndex + 1, list); postorderRec(2*nodeIndex + 2, list); list.add(heap[nodeIndex]) ; } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | //Traverse as tree postorder, Time O(n), Space O(n) postorder() { var output = []; this.postorderRec(0, output); return output; } //recursion helper, Time O(n), Space O(n) postorderRec(nodeIndex, output) { if (nodeIndex > this.length-1) return; this.postorderRec(2*nodeIndex + 1, output); this.postorderRec(2*nodeIndex + 2, output); output.push(this.heap[nodeIndex]); } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 | # Traverse as tree postorder, Time O(n), Space O(n) def postorder(self): output = [] self.postorderRec(0, output) return output # Recursion helper, Time O(n), Space O(n) def postorderRec(self, nodeIndex, output): if (nodeIndex > self.length-1): return self.postorderRec(2*nodeIndex + 1, output) self.postorderRec(2*nodeIndex + 2, output) output.append(self.heap[nodeIndex]) |
Free download
Download max-heap implementation in Java, JavaScript and Python
Data structures introduction PDF