A minimum spanning tree(MST) is a subset of a weighted undirected graph, in which edges that form a tree (no cycle graph) include every vertex in a graph, where the sum of the weights of all the edges in the tree is minimized. Kruskal’s algorithm is an algorithm to find MST in a weighted undirected graph using union-find.
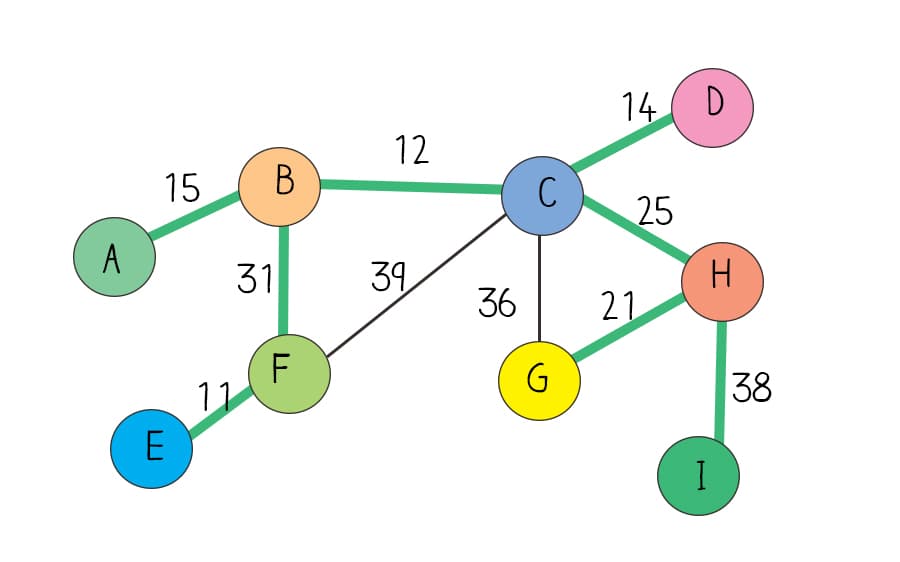
How does Kruskal’s algorithm work?
Kruskal’s algorithm is a greedy algorithm. In the process, it always adds the next lowest weight edge. In order not to form a cycle, it uses find and union methods in the DisjointSet class. If two vertices of an edge don’t share the same root confirmed by the find method, you add this edge to MST. After adding the edge, call the union method to union these two vertices so that they will not be added again.
Table of Content
Define an Edge classe
MST is a weighted graph problem. You can define edge as a class, in which there are source vertex, target vertex, and weight.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | static class GraphEdge<E> { E src, dest; int weight; //Time O(1), Space O(1) public GraphEdge(E src, E dest, int weight) { this.src = src; this.dest = dest; this.weight = weight; } //Time O(1), Space O(1) @Override public String toString() { return "(" + src + ", " + dest + ", " + weight + ")"; } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 | class GraphEdge { //Time O(1), Space O(1) constructor(src, dest, weight) { this.src = src; this.dest = dest; this.weight = weight; } //Time O(1), Space O(1) toString() { return "(" + this.src + ", " + this.dest + ", " + this.weight + ")"; } } |
Python
1 2 3 4 5 6 7 8 9 10 | class GraphEdge : #Time O(1), Space O(1) def __init__(self, src, dest, weight) : self.src = src self.dest = dest self.weight = weight #Time O(1), Space O(1) def __str__(self) : return "(" + str(self.src) + ", " + str(self.dest) + ", " + str(self.weight) + ")" |
Add edge
Next, you construct a graph. A graph is often represented as an adjacency list. Here a graph is simplified. You don’t need to create a hashmap to represent the graph. Instead, you define edges and vertices separately. edges is a list of GraphEdge objects. nodes is a set of individual vertices.
Java
1 2 3 4 5 6 7 8 9 10 11 12 | import java.util.*; @SuppressWarnings({ "unchecked", "rawtypes" }) public class Kruskal<T> { List<GraphEdge<T>> edges = new ArrayList<>(); Set<T> nodes = new HashSet<>(); //nodes in graph //Add node and edges, Time O(1), Space O(1) public void addEdge(T u, T v, int w) { nodes.add(u); nodes.add(v); edges.add(new GraphEdge<T>(u,v,w)); } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 | const DisjointSet = require('./DisjointSet.js') class Kruskal { constructor() { this.edges = new Array(); this.nodes = new Set(); //nodes in graph } //Add node and edges, Time O(1), Space O(1) addEdge(u, v, w) { this.nodes.add(u); this.nodes.add(v); this.edges.push(new GraphEdge(u,v,w)); } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 | import DisjointSet class Kruskal: # Time O(1), Space O(1) def __init__(self): self.edges = [] self.nodes = set() # Add node and edges, Time O(1), Space O(1) def addEdge(self, u, v, w) : self.nodes.add(u) self.nodes.add(v) self.edges.append(GraphEdge(u,v,w)) |
Kruskal’s algorithm
Now you can apply Kruskal’s algorithm. Since it uses the Disjoint set data structure’s union and find methods, you can create an object of the DisjointSet class, which has been introduced in the Disjoint set and union-find post. Call the makeSet method with nodes to establish a disjoint set. Sort the list of edges by their weights in ascending order. Starting from the smallest-weight edge, if the source node and target node are not in the same subset of a disjoint set, there is no cycle when adding them. You can add this edge to MST. Then you union these two nodes so that they will not be selected again.
The time complexity of Kruskal’s algorithm is O(E*logE) due to sorting, and E is the number of edges in the graph. Since find uses recursion, the space is required for the recursive function’s call stacks. The Space complexity is O(E*a(E+V)), where α(n) is the extremely slow-growing inverse Ackermann function due to the optimization of path compression and union by rank in disjoint set implementation.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | // Time O(E*log(E) Space O(E*a(E+V)), a(n) is the inverse ackermann function, public List<GraphEdge<T>> weightedMST() { List<GraphEdge<T>> mst = new ArrayList<>(); Collections.sort(edges, Comparator.comparingInt(e -> e.weight)); DisjointSet<T> ds = new DisjointSet(); ds.makeSet(new ArrayList(nodes)); for(GraphEdge<T> edge: edges) { if (!ds.find(edge.src).equals(ds.find(edge.dest)) ) { mst.add(edge); ds.union(edge.src, edge.dest); } } return mst; } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | // Time O(E*log(E)) Space O(E*a(E+V)), a(n) is the inverse ackermann function, weightedMST() { var mst = new Array(); this.edges.sort((a,b) => a.weight-b.weight); var ds = new DisjointSet(); ds.makeSet(this.nodes); for (let edge of this.edges) { if (ds.find(edge.src) != (ds.find(edge.dest)) ) { mst.push(edge); ds.union(edge.src, edge.dest); } } return mst; } |
Python
1 2 3 4 5 6 7 8 9 10 11 | # Time O(E*log(E) Space O(E*a(E+V)), a(n) is the inverse ackermann function, def kruskal(self): mst = [] ds = DisjointSet.DisjointSet() ds.make_set(list(self.nodes)) self.edges.sort(key = lambda x: x.weight) # sort edges by increasing weight for edge in self.edges: if ds.find(edge.src) != ds.find(edge.dest) : mst.append(edge) ds.union(edge.src, edge.dest) return mst |
Free download
Download Kruskal’s algorithm in Java, JavaScript
and Python
Minimum spanning tree (GitHub)