A binary search tree is an ordered binary tree. The left subtree contains nodes whose keys are less than the node’s key value, while the right subtree contains nodes whose keys are greater than or equal to the node’s key value. Moreover, both subtrees are also binary search trees. A binary search tree can retrieve data efficiently.
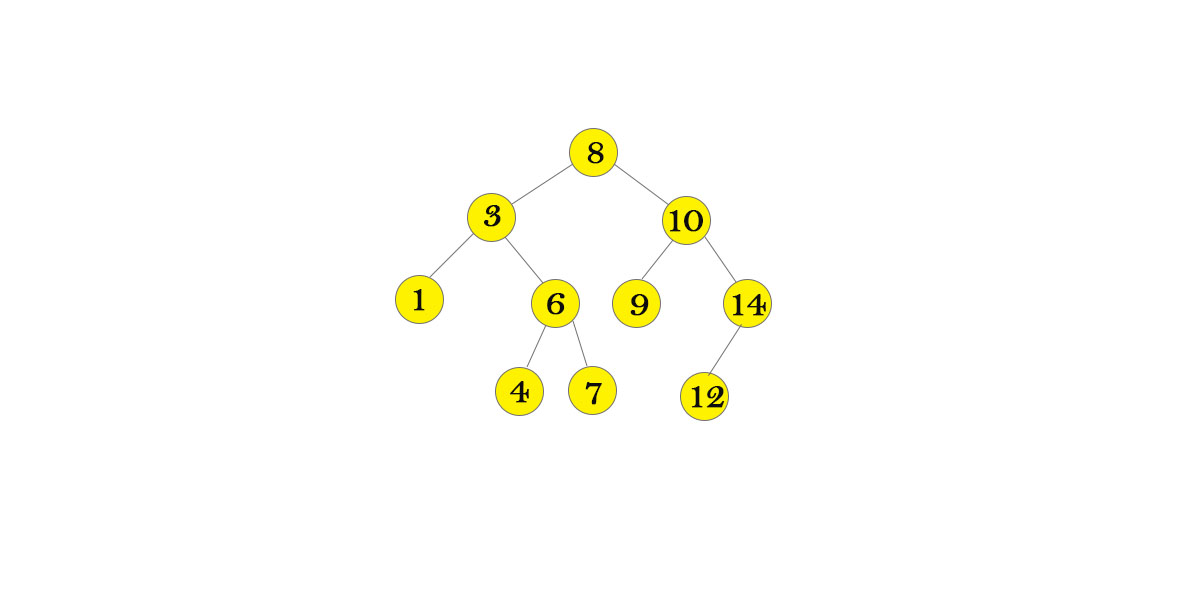
Table of Content
- Map of binary tree implementations
- Define classes
- Insert
- Delete by key
- Depth first search
- Breadth first search
- Free download
Map of binary tree implementations
Part 1 – Binary tree implementation
Part 2 – Binary search tree implementation
Part 3 – Binary search tree with parent pointer
Define classes
The TreeNode in the binary search tree is the same as the regular binary tree. It has three attributes, data, left, and right. data is the data stored in this node. Its data type can be anything such as Integer, String, or Object. left is the left child. right is the right child. Their data type is TreeNode.
After we define TreeNode, we can define the BinarySearchTree class. It has one attribute, root. It is the node from where most tree operations start.
Please note, since the binary search tree is ordered, in Java, BinarySearchTree’s generic data type extends the Comparable interface, so that we can compare data in insert, delete, or search operations.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | public class BinarySearchTree<T extends Comparable<T>> { static class TreeNode<T> { T data; TreeNode<T> left = null; TreeNode<T> right = null; //Override, Time O(1), Space O(1) @Override public String toString() { return String.valueOf(data); } } TreeNode<T> root = null; } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | class TreeNode { //Constructor, Time O(1), Space O(1) constructor() { this.left = null; this.right = null; } //Override, Time O(1), Space O(1) toString() { return this.data; } } class BinarySearchTree { //Constructor, Time O(1), Space O(1) constructor() { this.root = null; } } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | class TreeNode : #constructor, Time O(1) Space O(1) def __init__(self) : self.left = None self.right = None #Override, Time O(1), Space O(1) def __str__(self): return str(self.data) class BinarySearchTree : #constructor, Time O(1) Space O(1) def __init__(self) : self.root = None |
Insert
To insert a value into a binary search tree, we have to find the right spot. From the root, we compare the value with each node’s data. If the value is larger than the node’s data, we move to the right child. Otherwise move to the left child, until the node’s left or right child is null. Then we can add the new node with the input value as left or right child.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | //Insert a node based on value, Iteration, Time O(h) Space O(1), h is height of tree public void insert(T value) { TreeNode<T> newNode = new TreeNode<>(); newNode.data = value; if (root == null) { root = newNode; return; } TreeNode<T> curr = root; TreeNode<T> prev; while (true) { prev = curr; if (value.compareTo(curr.data) < 0) { curr = curr.left; if (curr == null) { prev.left = newNode; return; } } else { curr = curr.right; if (curr == null) { prev.right = newNode; return; } } } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | //Insert a node based on value, Iteration, Time O(h) Space O(1), h is height of tree insert(value) { var newNode = new TreeNode(); newNode.data = value; if (this.root == null) { this.root = newNode; return; } var curr = this.root; var prev; while (true) { prev = curr; if (value < curr.data) { curr = curr.left; if (curr == null) { prev.left = newNode; return; } } else { curr = curr.right; if (curr == null) { prev.right = newNode; return; } } } } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | #Insert a node based on value, Iteration, Time O(h) Space O(1), h is height of tree def insert(self, value) : newNode = TreeNode() newNode.data = value; if self.root == None: self.root = newNode return curr = self.root prev = None while (True) : prev = curr if value < curr.data : curr = curr.left if (curr == None) : prev.left = newNode return else : curr = curr.right if curr == None : prev.right = newNode return |
Doodle
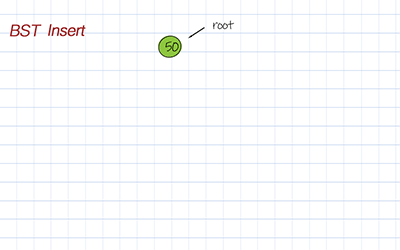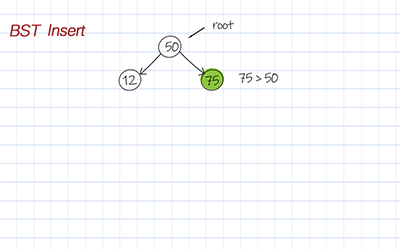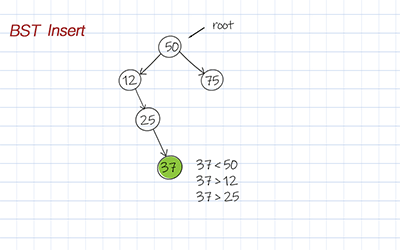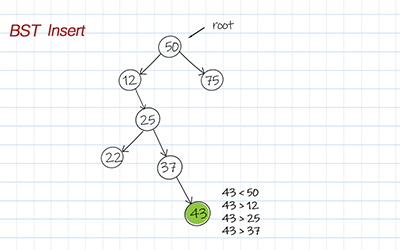
Delete by key
Deleting a node in a binary search tree is easier than deleting a node in a binary tree. We always promote the in-order successor of the deleted node. So it will be the right child’s leftmost descendent. If the right child is null, promote the left child.
Besides, we don’t need to go through all the nodes in the tree to search. We can just follow the path based on the comparison of the node’s data with the input key. So the time complexity is O(h), and h is the height of the tree.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | //Delete node by key, Iteration, Time O(h), Space O(1) public TreeNode<T> delete(T key) { if (root == null) return null; if (root.data == key) { root = getSuccessor(root); return root; } TreeNode<T> curr = root; while (true) { if (key.compareTo(curr.data) > 0) { if (curr.right == null || curr.right.data == key) { curr.right = getSuccessor(curr.right); break; } curr = curr.right; } else { if (curr.left == null || curr.left.data == key) { curr.left = getSuccessor(curr.left); break; } curr = curr.left; } } return root; } //Delete node, return next successor, Time O(h), Space O(1) private TreeNode<T> getSuccessor(TreeNode<T> node) { if (node == null) return null; if (node.right == null) return node.left; TreeNode<T> curr = node.right; while (curr.left != null) //find the left-most node curr = curr.left; curr.left = node.left; return node.right; } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | //Delete node by key, Iteration, Time O(h), Space O(1) delete(key) { if (this.root == null) return null; if (this.root.data == key) { this.root = this.getSuccessor(this.root); return this.root; } var curr = this.root; while (true) { if (key > curr.data) { if (curr.right == null || curr.right.data == key) { curr.right = this.getSuccessor(curr.right); break; } curr = curr.right; } else { if (curr.left == null || curr.left.data == key) { curr.left = this.getSuccessor(curr.left); break; } curr = curr.left; } } return this.root; } //Delete node, return next successor, Time O(h), Space O(1) getSuccessor(node) { if (node == null) return null; if (node.right == null) return node.left; var curr = node.right; while (curr.left != null) //find the left-most node curr = curr.left; curr.left = node.left; return node.right; } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | #Delete node by key, Iteration, Time O(h), Space O(1) def delete(self, key) : if self.root == None : return None if self.root.data == key : self.root = self.getSuccessor(self.root) return self.root curr = self.root; while True : if key > curr.data: if curr.right == None or curr.right.data == key : curr.right = self.getSuccessor(curr.right) break curr = curr.right else : if curr.left == None or curr.left.data == key: curr.left = self.getSuccessor(curr.left) break curr = curr.left return self.root #Delete node, return next successor, Time O(h), Space O(1) def getSuccessor(self, node) : if node == None: return None if node.right == None : return node.left curr = node.right while curr.left != None: #find the left-most node curr = curr.left curr.left = node.left return node.right |
Doodle
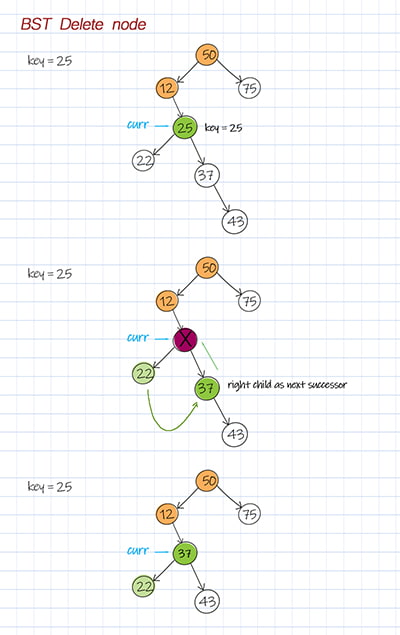
Depth first search
There are two ways to search, Depth first search and Breadth first search.
Depth-first search (DFS) starts from the root and explores the child nodes as far as possible before backtracking. DFS is usually implemented with recursion or stack.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 | //Depth first search, recursion, Time O(h), Space O(h) TreeNode<T> searchDFS(T key) { return dfsHelper(root, key); } //Search recursion helper, Time O(h), Space O(h) public TreeNode<T> dfsHelper(TreeNode<T> node, T key) { if(node == null) return null; if(node.data == key) return node; return key.compareTo(node.data) > 0 ? dfsHelper(node.right, key) : dfsHelper(node.left, key); } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 | //Depth first search, recursion, Time O(h), Space O(h) searchDFS(key) { return this.dfsHelper(this.root, key); } //Search recursion helper, Time O(h), Space O(h) dfsHelper(node, key) { if(node == null) return null; if(node.data == key) return node; return key> node.data ? this.dfsHelper(node.right, key) : this.dfsHelper(node.left, key); } |
Python
1 2 3 4 5 6 7 8 9 10 11 | #Depth first search, recursion, Time O(h), Space O(h) def searchDFS(self, key) : return self.dfsHelper(self.root, key); #Search recursion helper, Time O(h), Space O(h) def dfsHelper(self, node, key) : if node == None: return None if node.data == key: return node return self.dfsHelper(node.right, key) if key> node.data else self.dfsHelper(node.left, key) |
Breadth first search
Breath First Search (BFS) starts from the root and explores all its children before going to the next level. BFS is usually implemented with Queue.
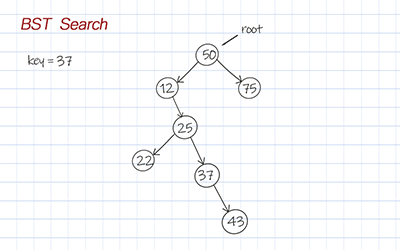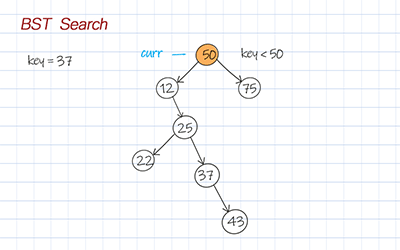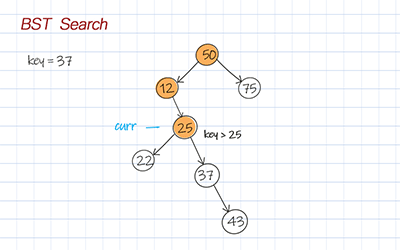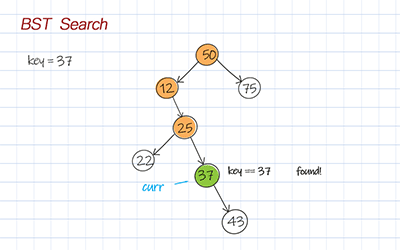
Both DFS and BFS in the binary search tree have a time complexity of O(h). The search doesn’t need to go through all the nodes in the tree. It follows the path based on the comparison of the node’s data with the input key.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 | //Iteration, Time O(h), Space O(1) public TreeNode<T> searchBFS(T key) { TreeNode<T> curr = root; while (curr!= null) { if (curr.data == key) return curr; else if (key.compareTo(curr.data) < 0) curr = curr.left; else curr = curr.right; } return curr; } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 | //Iteration, Time O(h), Space O(1) searchBFS(key) { var curr = this.root; while (curr!= null) { if (curr.data == key) return curr; else if (key < curr.data) curr = curr.left; else curr = curr.right; } return curr; } |
Python
1 2 3 4 5 6 7 8 9 10 11 | #Iteration, Time O(h), Space O(1) def searchBFS(self, key) : curr = self.root while curr!= None : if curr.data == key: return curr elif key < curr.data: curr = curr.left else : curr = curr.right return curr |
Doodle
Free download
Download binary search tree implementation in Java, JavaScript and Python
Data structures illustration PDF
You may also like
What is the time complexity of binary search tree time?
The time complexity of insertion, deletion, and search in a binary search tree is O(h), where h is the height of the tree. When the tree is balanced, the time complexity is O(logn).
