Topological sort is one of the graph problems. It is to find the order of vertices in a directed graph based on the edge directions. For example, an edge [uv] starts from u and ends at v. Another edge [mn] starts from m and ends at n. After applying topological sort, the sequence of vertices (u, v, m, n ) should satisfy all edge directions. In the following diagram, there are 5 edges. The sequence of (A, B, C, D, E) satisfies all directions of edges.
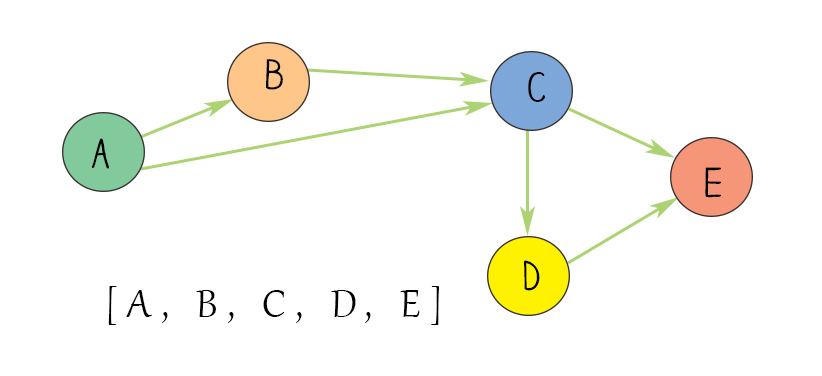
Topological sort can be only applied to a directed graph that doesn’t have a cycle, called a Directed Acyclic Graph(DAG). There are a few algorithms to implement topological sort. The commonly used ones are Depth-first search and Kahn’s algorithm. The results are not necessarily unique. But they all should meet the criteria to satisfy the edge directions.
Since it is a graph problem, you can make use of the existing Graph class. Use the addEdge method in the Graph class so that you can create a graph quickly. In both DFS and Kahn’s algorithm, use a graph object as the input. The output is the list of vertices that is a topological sort list.
Table of Content
Topological Sort DFS
Depth-first search is the same as depth-first search in a graph traversal. Starting from the source node, you call the recursive method to visit its neighbor’s neighbor until call back. It uses a variable visited to track whether the node has been visited so that each node is visited once.
Another variable stack is used to store the result. After a recursive function returns, that means the node has reached the state that there are no unvisited target nodes in its neighbors. Push this node in the stack. At the end, reverse the stack, you will get the result.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | import java.util.*; //DFS wrapper, Time O(V+E), Space O(V), //V is number of vertices, E is number of edges public List<T> topoSortDfs(Graph<T> g) { Stack<T> stack = new Stack<>(); Map<T, Boolean> visited = new HashMap<>(); for (T key: g.adj.keySet()) visited.put(key, false); for (T key: g.adj.keySet()) { if (visited.get(key) == false) dfsHelper(g, key, visited, stack); //call recursion } List<T> res = new ArrayList<>(); while (stack.empty() == false) //get result res.add(stack.pop()); return res; } //DFS recursion, Time O(V+E), Space O(V) private void dfsHelper(Graph<T> g, T v, Map<T, Boolean> visited, Stack<T> stack) { visited.put(v, true); for (T i: g.adj.get(v)) { if (!visited.get(i)) //make sure visit once dfsHelper(g, i, visited, stack); } stack.push(v); //push source node } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | const Graph = require('./Graph.js') //DFS, use stack, Time O(V+E), Space O(V), V is number of nodes, E is number of edges function topoSortDfs(g) { var stack = []; var visited = new Map(); for (let k of g.adj.keys()) visited.set(k, false); for (let k of g.adj.keys()) { if (visited.get(k) == false) dfsHelper(g, k, visited, stack); //call resursion } var res = new Array(); while (stack.length > 0) //get result res.push(stack.pop()); return res; } //DFS helper, Time O(V+E), Space O(V) function dfsHelper(g, v, visited, stack) { visited.set(v, true); for (let i of g.adj.get(v)) { if (!visited.get(i)) dfsHelper(g, i, visited, stack); } stack.push(v); } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | import Graph # Time O(V+E), Space (V) def topoSortDfs(g) : stack = []; visited = {}; for k in g.adj.keys(): visited[k] = False; for k in g.adj.keys(): if visited[k] == False: dfsHelper(g, k, visited, stack) #call recursion res = [] while len(stack) > 0: #get result res.append(stack.pop()) return res # DFS helper, Time O(V+E), Space O(V) def dfsHelper(g, v, visited, stack) : visited[v] = True for i in g.adj.get(v) : if visited[i] == False: dfsHelper(g, i, visited, stack); stack.append(v); |
Kahn’s algorithm (BFS)
Kahn’s algorithm uses indegree and queue data structures. indegree is a hash map of all nodes and their counts. If a node is in another node’s neighbors, its indegree count increases by 1. If a node’s in-degree count is 0, this node has no target nodes in its neighbors. It is the start node. Put this node in the queue.
Next use BFS by taking out the first item in the queue. Put it in the result list. Then use the for loop to check its target nodes and reduce the target node’s indegree count by 1. When the node’s indegree count is 0, you can add the node to the queue. In the end, when the result list has all the nodes in a graph, you can return the result.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | //BFS, Kahn's algorithm, Time O(V+E), space O(V+E), public List<T> topoSortBfs(Graph<T> g) { Map<T, Integer> indegree = new HashMap<T, Integer>(); for (T c: g.adj.keySet()) indegree.put(c,0); for (T from: g.adj.keySet()) { LinkedList<T> ne = g.adj.get(from); for (T to: ne) { indegree.put(to, indegree.get(to)+1); //count the target nodes number } } Queue<T> q = new LinkedList<T>(); for (T c: indegree.keySet()) if(indegree.get(c) == 0) // a source nodes that has no tagert node q.add(c); List<T> res = new ArrayList<>(); while (!q.isEmpty()) { T from = q.remove(); res.add(from); //add to result if (g.adj.containsKey(from)) { for (T to: g.adj.get(from)) { indegree.put(to, indegree.get(to)-1); //decrease indegree by 1 first if (indegree.get(to) == 0) q.add(to); } } } if (res.size() == g.adj.size()) //complete all nodes return res; return null; } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | //BFS Kahn’s algorithm, use indegree, Time O(V+E), Space O(V) function topoSortBfs(g) { var indegree = new Map(); for (let key of g.adj.keys()) indegree.set(key, 0); for(let key of g.adj.keys()) { let to = g.adj.get(key); for(let node of to) { indegree.set(node, indegree.get(node)+1);//count the target nodes number } } var queue = new Array(); for(let key of g.adj.keys()) { if(indegree.get(key) == 0) // a source nodes that has no tagert node queue.push(key); } var res = new Array(); while(queue.length != 0) { let u = queue.shift(); res.push(u); for(let node of g.adj.get(u)) { indegree.set(node, indegree.get(node)-1); //decrease indegree by 1 if (indegree.get(node) == 0) { queue.push(node); } } } if (res.length == g.adj.size) { //result has all nodes return res; } return null; } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | # Kahn’s algorithm, use indegree, Time O(V+E), Space O(V) def topoSortBfs(g) : indegree = {}; for key in g.adj.keys(): indegree[key] = 0 for key in g.adj.keys(): to = g.adj[key]; for node in to: indegree[node]= indegree[node]+1 #count the target nodes number queue = [] for key in g.adj.keys() : if indegree.get(key) == 0 : # a source nodes that has no tagert node queue.append(key); res = [] while queue: u = queue.pop() res.append(u) for node in g.adj[u]: indegree[node] = indegree[node]-1 #decrease indegree by 1 if indegree[node] == 0: queue.append(node) if len(res) == len(g.adj): #complete all nodes return res return None |
Free download
Download Topological sort in Java, JavaScript
and Python
Topological sort to find ranking
What is Kahn’s algorithm?
Kahn’s algorithm is an algorithm useing breadth-first search to find topological sort in a directed graph. Kahn’s algorithm uses a graph’s indegree and a queue data structure.