Quicksort uses the divide and conquer technique to provide fast sorting. Divide-and-conquer is a technique works by recursively breaking down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The quick sort gif uses animation to explain how quicksort works.
How quicksort works?
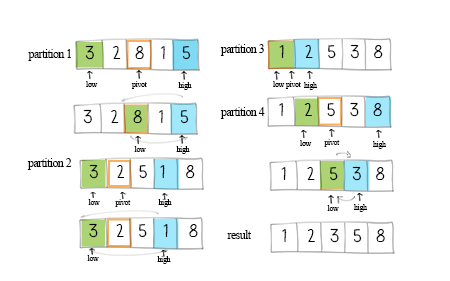
Quicksort calls a partition method to divide the array into two subarrays. This method returns an index for partition. Then the sorting method calls itself twice to sort these two subarrays.
What is the complexity of quicksort?
Quicksort operates in O(nlogn) time. It is faster than simple sorting O(n^2). The space complexity is O(logn), which is better than merge sort’s O(n). The space is used for recursion’s call stacks.
Quick sort gif
Quicksort implementation
The key part of the solution is the partition method. The variable pivot determines when to swap unordered elements. Its initial value can be the first, last or the middle item in the subarray. In this solution, the pivot is the middle of the array. The formula of its index is mid=low+(high-low)/2.
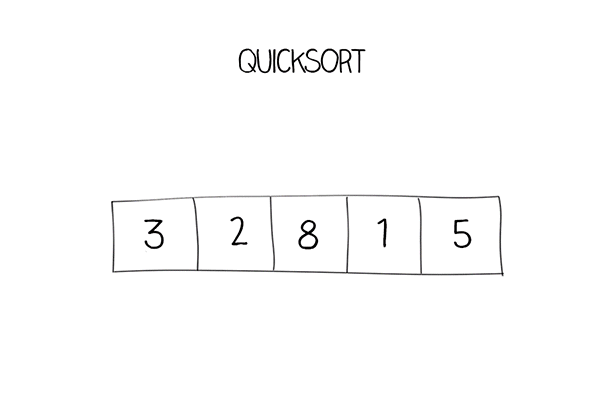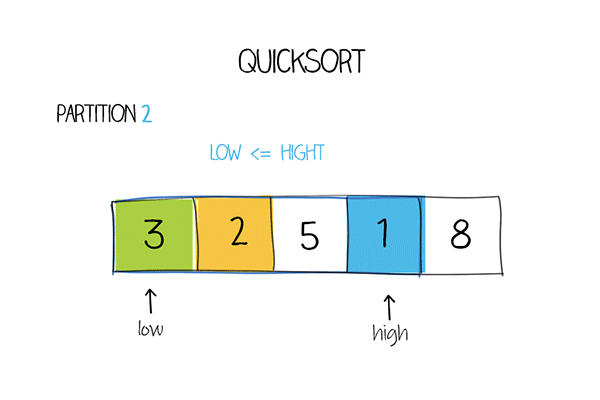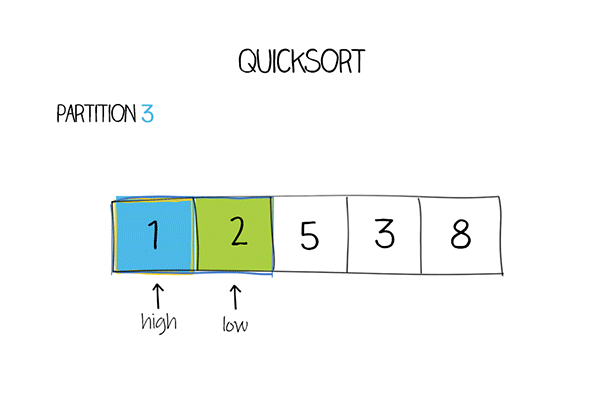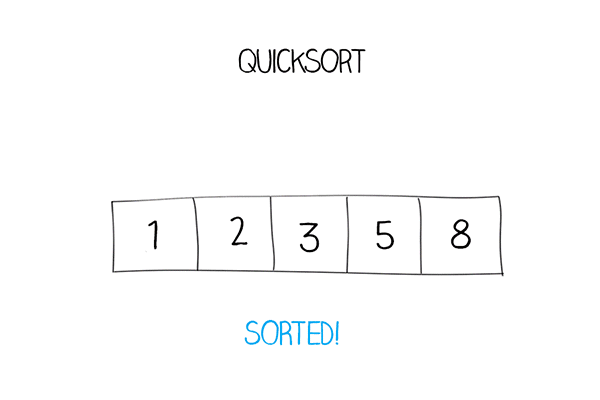
There are two pointers, low points to the first element. high points to the last element. Increase the low pointer if the values it points are less than the pivot. Decrease the high pointer if the values are larger than the pivot. After moving the pointers, if the low pointer is still less equal than the high pointer, swap the elements in the array. After each partition, either the largest element swaps to the right, or the smallest element swaps to the left.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | import java.util.Arrays; public class QuickSort { //Divide and conquer, Time worst O(n^2) average O(n*logn), Space O(logn), n is array length public static void quickSort(int[] a, int low, int high) { int index = partition(a, low, high); if (low < index-1) quickSort(a, low, index-1); if (index < high) quickSort(a, index, high); } //Partition, Time O(n), Space O(1) private static int partition(int[] a, int low, int high) { int mid = low + (high-low)/2; //middle of the array int pivot = a[mid]; while (low <= high) { while (a[low] < pivot) low ++; while (a[high] > pivot) high --; if (low <= high) { swap(a, low, high); low ++; high --; } } return low; } //Swap two elements by index, Time O(1), Space O(1) private static void swap(int[] a, int i, int j) { int tmp = a[i]; a[i] = a[j]; a[j] = tmp; } public static void main(String[] args) { int[] a = {19, 33, 4 , 61, 5, 38, -36, 21, 0}; quickSort(a, 0, a.length-1 ); System.out.print("Quick sort: "); System.out.println(Arrays.toString(a)); } } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | //Divide and conquer, Time worst O(n^2) average O(n*logn), Space O(logn), n is array length function quickSort(a, low, high) { var index = partition(a, low, high); if (low < index-1) quickSort(a, low, index-1); if (index < high) quickSort(a, index, high); } //Partition, Time O(n), Space O(1) function partition(a, low, high) { var mid = Math.floor(low + (high-low)/2); //middle of the array var pivot = a[mid]; while (low <= high) { while (a[low] < pivot) low ++; while (a[high] > pivot) high --; if (low <= high) { swap(a, low, high); low ++; high --; } } return low; } //Swap two elements by index, Time O(1), Space O(1) function swap(a, i, j) { var tmp = a[i]; a[i] = a[j]; a[j] = tmp; } var a = [19, 33, 4 , 61, 5, 38, -36, 21, 0]; quickSort(a, 0, a.length-1 ); console.log("Quick sort: " + a); |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | #Divide and conquer, Time worst O(n^2) average O(n*logn), Space O(logn), n is array length def quickSort(a, low, high): index = partition(a, low, high) if low < index-1: quickSort(a, low, index-1) if index < high : quickSort(a, index, high) #Partition, Time O(n), Space O(1) def partition(a, low, high) : mid = int(low + (high-low)/2) #middle of the array pivot = a[mid] while (low <= high) : while (a[low] < pivot) : low += 1 while (a[high] > pivot): high -= 1 if (low <= high) : swap(a, low, high) low += 1 high -= 1 return low #Swap two elements by index, Time O(1), Space O(1) def swap(a, i, j) : tmp = a[i] a[i] = a[j] a[j] = tmp a = [19, 33, 4 , 61, 5, 38, -36, 21, 0] print(a) quickSort(a, 0, len(a)-1 ) print("Quick sort: ") print(a) |
Doodle
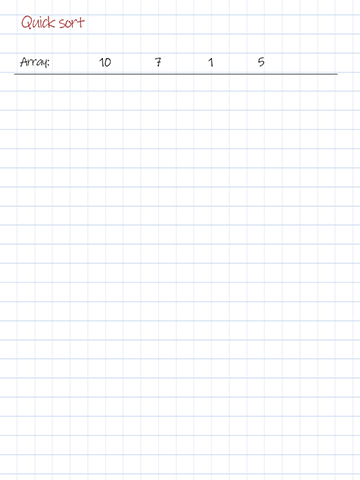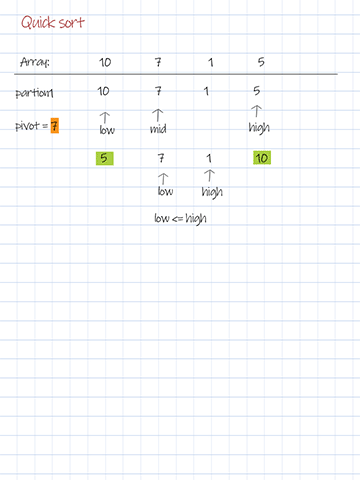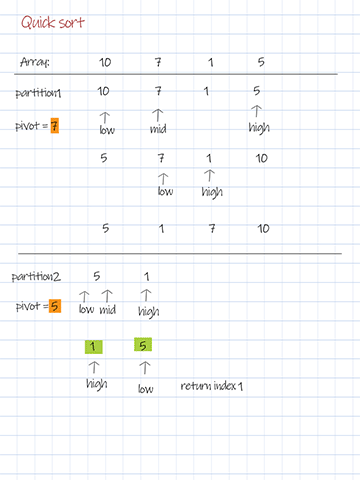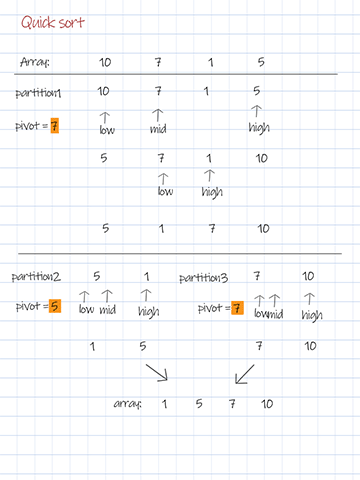
Download
Download quicksort in Java, JavaScript and Python
Algorithm types and algorithm examples