A tree is a hierarchical data structure. It consists of nodes with a root node at the top and a subtree of children nodes. The nodes are connected by edges. Each parent node can point to null, one, or multiple nodes. A tree is an instance of a more general data structure called a graph. It has no cycles.
A binary tree has at most two children, we name them left child and right child. Each node has a value associated with it. They are not in a particular order. The time complexity of most binary tree operations is O(n) in the worst case.
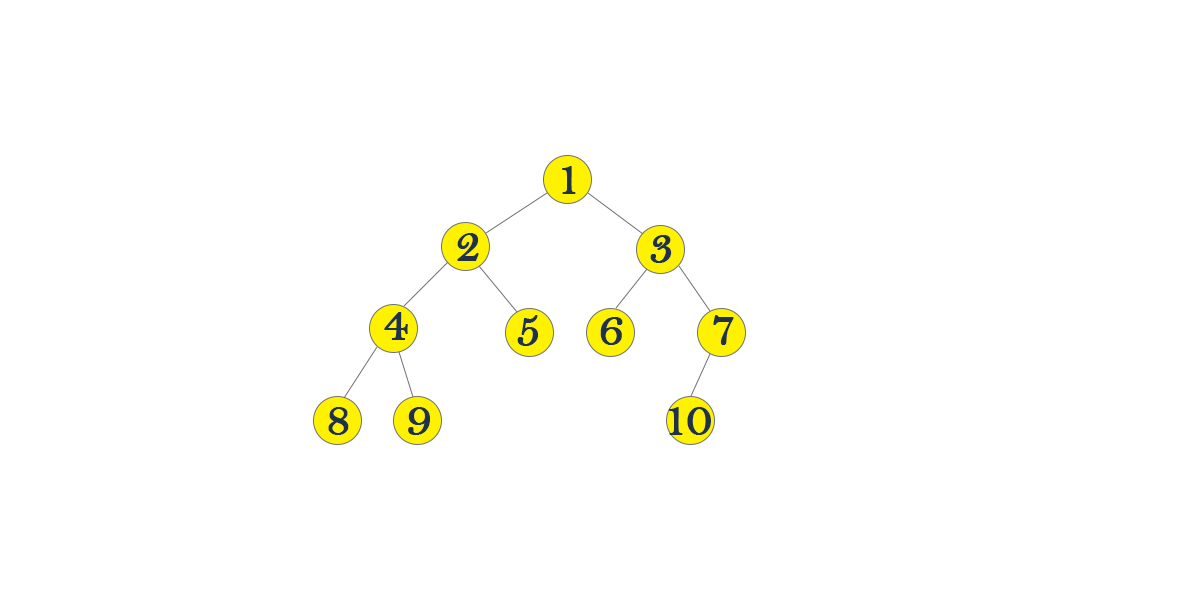
Table of Content
- Map of binary tree implementations
- Define classes
- Add child
- Delete by key
- Depth first search
- Breadth first search
- Inorder traversal
- Preorder traversal
- Postorder traversal
- Leverorder traversal
- Free download
Map of binary tree implementations
Part 1 – Binary tree implementation
Part 2 – Binary search tree implementation
Part 3 – Binary search tree with parent pointer
Define classes
A binary tree consists of nodes. The first thing is to define the TreeNode. It has three attributes, data, left, and right. data is the data stored in this node. Its data type can be anything such as Integer, String, or Object. left is the left child. right is the right child. Their data type is TreeNode.
After we define TreeNode, we can define the BinaryTree class. It has one attribute, root. root is at the node at the top of the tree. It is the node from where most tree operations start.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
class TreeNode<T> { T data; TreeNode<T> left = null; TreeNode<T> right = null; //Constructor, Time O(1), Space O(1) public TreeNode(T value) { this.data = value; } //Override, Time O(1), Space O(1) @Override public String toString() { return String.valueOf(data); } } public class BinaryTree<T> { TreeNode<T> root = null; } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
class TreeNode { //Constructor, Time O(1), Space O(1) constructor(val) { this.data = val; this.left = null; this.right = null; } //Override, Time O(1), Space O(1) toString() { return this.data; } } class BinaryTree { //Constructor, Time O(1), Space O(1) constructor() { this.root = null; } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
class TreeNode : #Constructor, Time O(1), Space O(1) def __init__(self,val) : self.data = val self.left = None self.right = None #Override, Time O(1), Space O(1) def __str__(self): return str(self.data) class BinaryTree : #Constructor, Time O(1), Space O(1) def __init__(self) : self.root = None |
Add child
Since all the nodes in the binary tree are not ordered in any way, we can add the left and right child directly to any node. If there are children for this node already, this method simply replaces the children with new ones.
Java
|
1 2 3 4 5 |
//add children, Time O(1) Space O(1) public void addChild(TreeNode<T> p, TreeNode<T> l, TreeNode<T> r) { p.left = l; p.right =r; } |
Javascript
|
1 2 3 4 5 |
//add children, Time O(1) Space O(1) addChild(p, l, r) { p.left = l; p.right = r; } |
Python
|
1 2 3 4 |
#add children, Time O(1) Space O(1) def addChild(self, p, l, r) : p.left = l p.right = r |
Doodle
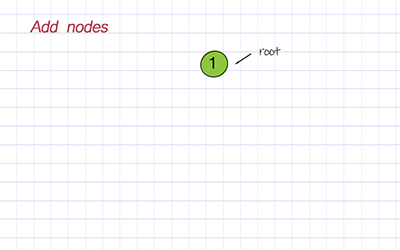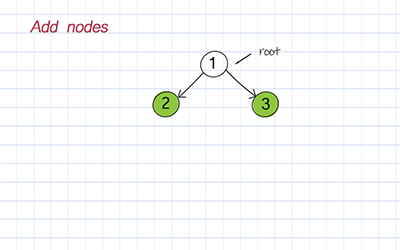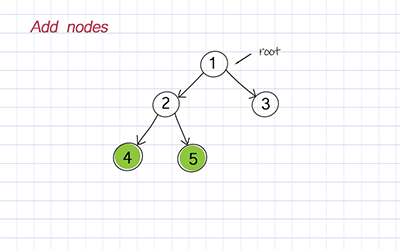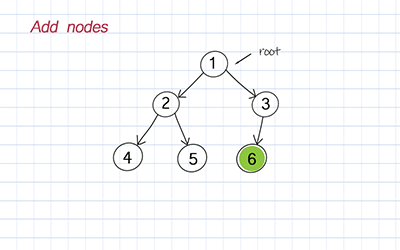
Delete by key
Delete node is the most complicated operation in the tree. We have to find the node that matches the key and find the successor so that the parent of the deleted node can connect to its successor.
Since a binary tree is not ordered, there are two cases to consider the successor, either promote the left child as the replacement or promote the right child to be the replacement.
To promote the left child as successor, the right child of the deleted node will be linked to the rightmost child of the left child. On the other hand, to promote the right child as a successor, the left child of the deleted node will be linked to the leftmost child of the right child. Two methods are created to deal with different cases. You can select which one to use based on your design.
To search all nodes of the tree for the key, we use recursion. In the recursion wrapper method, check the key with the root’s data. If matched, we have to reset the root to point to its successor. In the recursion helper method, check the cases such as whether the node is a leaf, has one child, or has two children. Then call itself with left or right child node.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
//Delete node by key, Recursion, Time O(n), Space O(n), n is number of nodes in tree public TreeNode<T> delete(T key) { if (root == null ) return null; if (root.data == key) { //delete root root = getSuccessorLeftFirst(root); return root; } deleteHelper(root, key); return root; } //delete recursion helper, Time O(n) Space O(n) private void deleteHelper(TreeNode<T> node, T key) { if (node == null ) return; if (node.data == key && node.left==null && node.right == null) { //delete leaf node = null; return; } else if ( node.right!= null && node.right.data == key) { node.right = getSuccessorLeftFirst(node.right); return; } else if (node.left != null && node.left.data == key) { node.left = getSuccessorLeftFirst(node.left); return; } if (node.left != null) deleteHelper(node.left, key); if (node.right != null) deleteHelper(node.right,key); } //get next node of the deleted node, left child as successor, Time O(h), Space O(1) //h is height of tree TreeNode<T> getSuccessorLeftFirst(TreeNode<T> node) { if (node == null) return null; if (node.left == null) return node.right; TreeNode<T> curr = node.left; while (curr.right != null) //find the right-most node curr = curr.right; curr.right = node.right; return node.left; } //get next node of the deleted node, right child as successor, Time O(h), Space O(1) TreeNode<T> getSuccessorRightFirst(TreeNode<T> node) { if (node == null) return null; if (node.right == null) return node.left; TreeNode<T> curr = node.right; while (curr.left != null) //find the left-most node curr = curr.left; curr.left = node.left; return node.right; } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
//Delete node by key, Recursion, Time O(n), Space O(n), n is number of nodes in tree delete(key) { if (this.root == null ) return null; if (this.root.data == key) { //delete root this.root = this.getSuccessorLeftFirst(this.root); return this.root; } this.deleteHelper(this.root, key); return this.root; } //detele recursion helper, Time O(n) Space O(n) deleteHelper(node, key) { if (node == null ) return; if (node.data == key && node.left == null && node.right == null) { //delete leaf node = null; return; } else if ( node.right != null && node.right.data == key) { node.right = this.getSuccessorLeftFirst(node.right); return; } else if (node.left != null && node.left.data == key) { node.left = this.getSuccessorLeftFirst(node.left); return; } if (node.left != null) this.deleteHelper(node.left, key); if (node.right != null) this.deleteHelper(node.right,key); } //get next node of the deleted node, left child as successor, Time O(h), Space O(1) //h is height of tree getSuccessorLeftFirst(node) { if (node == null) return null; if (node.left == null) return node.right; var curr = node.left; while (curr.right != null) //find the right-most node curr = curr.right; curr.right = node.right; return node.left; } //get next node of the deleted node, right child as successor, Time O(h), Space O(1) getSuccessorRightFirst(node) { if (node == null) return null; if (node.right == null) return node.left; var curr = node.right; while (curr.left != null) //find the left-most node curr = curr.left; curr.left = node.left; return node.right; } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
#Delete node by key, Recursion, Time O(n), Space O(n), n is number of nodes in tree def delete(self, key) : if self.root == None: return None if (self.root.data == key) : #delete root self.root = self.getSuccessorLeftFirst(self.root) return self.root self.deleteHelper(self.root, key) return self.root #delete recursion helper, Time O(n) Space O(n) def deleteHelper(self, node, key) : if node == None: return if (node.data == key and node.left == None and node.right == None) : #delete leaf node = None return elif node.right != None and node.right.data == key : node.right = self.getSuccessorLeftFirst(node.right) return elif node.left != None and node.left.data == key : node.left = self.getSuccessorLeftFirst(node.left) return if node.left != None: self.deleteHelper(node.left, key) if node.right != None: self.deleteHelper(node.right,key) #get next node of the deleted node, left child as successor, Time O(h), Space O(1) #h is height of tree def getSuccessorLeftFirst(self, node) : if node == None : return None if node.left == None: return node.right curr = node.left while curr.right != None: #find the right-most node curr = curr.right; curr.right = node.right return node.left #get next node of the deleted node, right child as successor, Time O(h), Space O(1) def getSuccessorRightFirst(self, node): if node == None: return None if node.right == None: return node.left curr = node.right while curr.left != None: #find the left-most node curr = curr.left curr.left = node.left return node.right |
Doodle 1
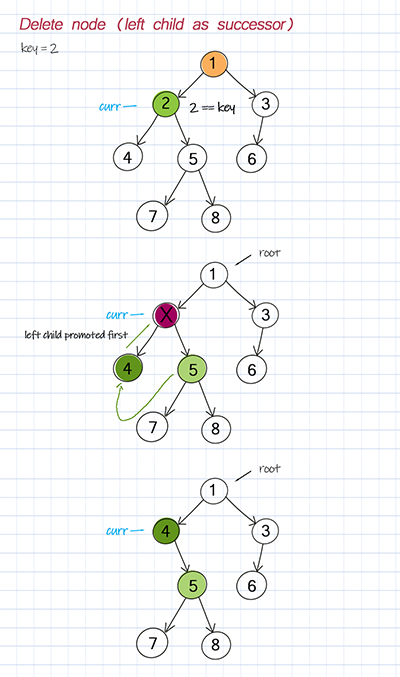
Doodle 2
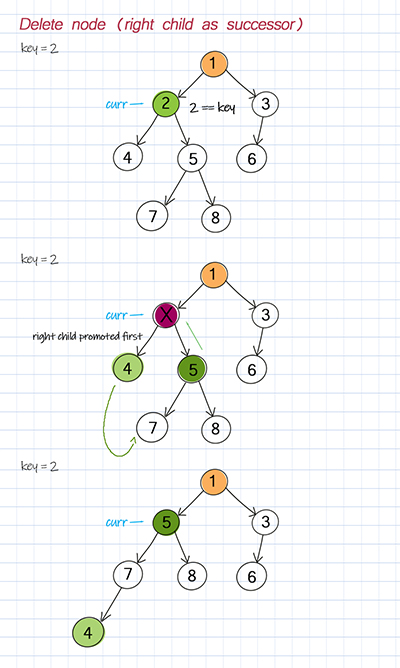
Depth first search (DFS)
There are two ways of searching: depth-first search and breadth-first search. Depth-first search (DFS) starts from the root and explores the child nodes as far as possible before backtracking. DFS is usually implemented with recursion or stack.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
//Depth first search, Recursion, Time O(n) Space O(n) public TreeNode<T> searchDFS(T key) { return dfsHelper(root, key); } //Search recursion helper, Time O(n), Space O(n) private TreeNode<T> dfsHelper(TreeNode<T> node, T value) { if (node == null) return null; if (value == node.data) return node; TreeNode<T> left = dfsHelper(node.left, value); TreeNode<T> right = dfsHelper(node.right, value); return left != null ? left : right; } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
//Depth first search, Recursion, Time O(n) Space O(n) searchDFS(key) { return this.dfsHelper(this.root, key); } //Search recursion helper, Time O(n), Space O(n) dfsHelper(node, key) { if (node == null) return null; if (key == node.data) return node; var left = this.dfsHelper(node.left, key); var right = this.dfsHelper(node.right, key); return left != null ? left : right; } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
#Depth first search, Recursion, Time O(n) Space O(n) def searchDFS(self, key) : return self.dfsHelper(self.root, key) #Search recursion helper, Time O(n), Space O(n) def dfsHelper(self, node, key) : if node == None: return None if key == node.data: return node left = self.dfsHelper(node.left, key) right = self.dfsHelper(node.right, key) return left if left != None else right |
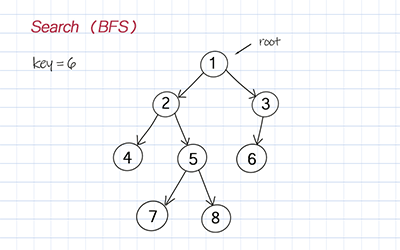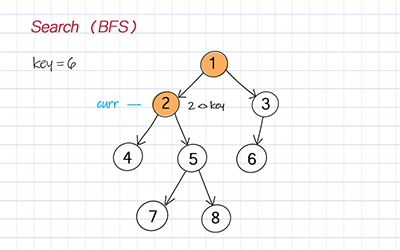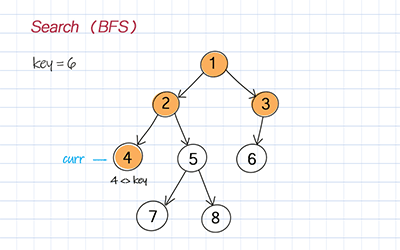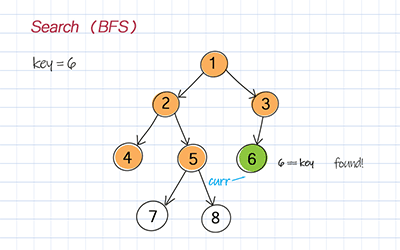
Breadth first search (BFS)
Breath First Search (BFS) starts from the root and explores all its children before going to the next level. BFS is usually implemented with Queue.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
//Breadth first search, Iteration, Time O(n), Space O(n) public TreeNode<T> searchBFS(T key) { if (root == null) return null; Queue<TreeNode<T>> q = new LinkedList<TreeNode<T>>(); q.add(root); while (!q.isEmpty()) { TreeNode<T> curr = q.poll(); if (curr.data == key) return curr; if (curr != null) { if (curr.left != null) q.add(curr.left); if (curr.right != null) q.add(curr.right); } } return null; } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
//Breadth first search, Iteration, Time O(n), Space O(n) searchBFS(key) { if (!this.root) return null let queue = [this.root] while (queue.length > 0) { let curr = queue.pop() if (curr.data == key) return curr; if (curr.left) queue.unshift(curr.left) if (curr.right) queue.unshift(curr.right) } return null } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
#Breadth first search, Iteration, Time O(n), Space O(n) def searchBFS(self, key) : if self.root == None: return None queue = [self.root] while (len(queue) > 0) : curr = queue.pop(0) if curr.data == key: return curr if curr.left is not None: queue.append(curr.left) if curr.right is not None: queue.append(curr.right) return None |
Doodle
Inorder traversal
Traversal is to visit all nodes in the tree in some specified order. While visiting, we can either print or save their values to an output list. Similar to search, we use depth-first search or breadth-first search methods.
For depth-first search, there are three ways: inorder, preorder, and postorder. They can be implemented using recursion and stack. In this post, we use recursion to implement DFS.
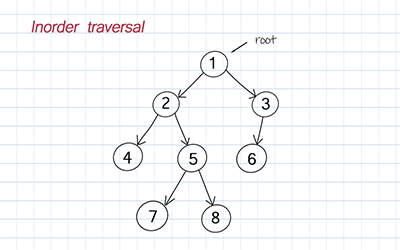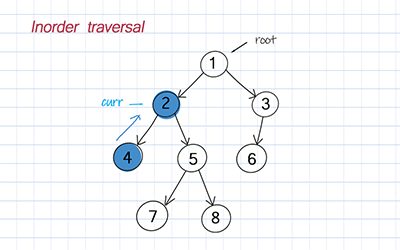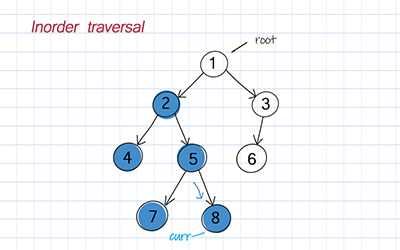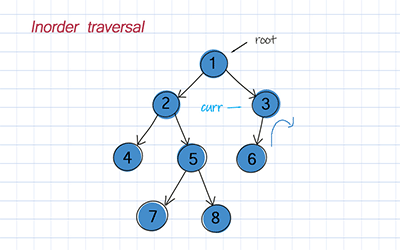
Inorder is to traverse the left subtree, visit the root, and traverse the right subtree.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
//Inorder traversal, Recursion, Time O(n), Space O(n) //n is number of nodes in trees public List<T> inorder() { List<T> list = new ArrayList<>(); inorderRec(root, list); return list; } //Inorder recursion helper, Time O(n), Space O(n) private void inorderRec(TreeNode<T> node, List<T> list) { if (node == null) return; inorderRec(node.left, list); list.add(node.data); inorderRec(node.right, list); } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
//Inorder traversal, Recursion, Time O(n), Space O(n) //n is number of nodes in trees inorder() { var list = []; this.inorderRec(this.root, list); return list; } //Inorder recursion helper, Time O(n), Space O(n) inorderRec(node, list) { if (node == null) return; this.inorderRec(node.left, list); list.push(node.data); this.inorderRec(node.right, list); } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
#Inorder traversal, Recursion, Time O(n), Space O(n) #n is number of nodes in trees def inorder(self) : list = [] self.inorderRec(self.root, list) return list #Inorder recursion helper, Time O(n), Space O(n) def inorderRec(self, node, list) : if node == None: return self.inorderRec(node.left, list) list.append(node.data) self.inorderRec(node.right, list) |
Doodle
Preorder traversal
Preorder is to visit the root, traverse the left subtree, and traverse the right subtree.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
//Preorder traversal, Recursion, Time O(n), Space O(n) public List<T> preorder() { List<T> list = new ArrayList<>(); preorderRec(root, list); return list; } //Preorder recursion helper, Time O(n), Space O(n) private void preorderRec(TreeNode<T> node, List<T> list) { if (node == null) return; list.add(node.data); preorderRec(node.left, list); preorderRec(node.right, list); } |
JavaScript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
//Preorder traversal, Recursion, Time O(n), Space O(n) preorder() { var list = []; this.preorderRec(this.root, list); return list; } //preorder recursion helper, Time O(n), Space O(n) preorderRec(node, list) { if (node == null) return; list.push(node.data); this.preorderRec(node.left, list); this.preorderRec(node.right, list); } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
#Preorder traversal, Recursion, Time O(n), Space O(n) def preorder(self) : list = [] self.preorderRec(self.root, list) return list #Preorder recursion helper, Time O(n), Space O(n) def preorderRec(self, node, list) : if node == None: return list.append(node.data) self.preorderRec(node.left, list) self.preorderRec(node.right, list) |
Doodle
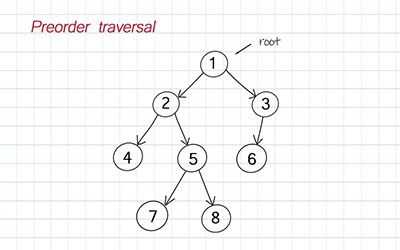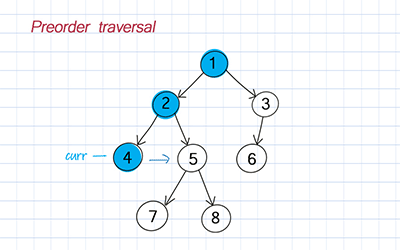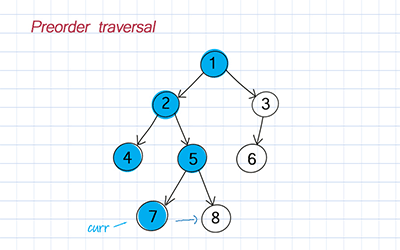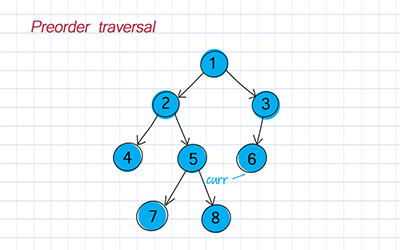
Postorder traversal
Postorder is to traverse the left subtree, traverse the right subtree, and visit the root.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
//Postorder traversal, Recursion, Time O(n), Space O(n) public List<T> postorder() { List<T> list = new ArrayList<>(); postorderRec(root, list); return list; } //Postorder recursion helper, Time O(n), Space O(n) private void postorderRec(TreeNode<T> node, List<T> list) { if (node == null) return; postorderRec(node.left, list); postorderRec(node.right, list); list.add(node.data); } |
JavaScript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
//Postorder traversal, Recursion, Time O(n), Space O(n) postorder() { var list = []; this.postorderRec(this.root, list); return list; } //Postorder recursion helper, Time O(n), Space O(n) postorderRec(node, list) { if (node == null) return; this.postorderRec(node.left, list); this.postorderRec(node.right, list); list.push(node.data); } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
#Postorder traversal, Recursion, Time O(n), Space O(n) def postorder(self) : list = [] self.postorderRec(self.root, list) return list #Postorder recursion helper, Time O(n), Space O(n) def postorderRec(self, node, list) : if node == None: return self.postorderRec(node.left, list) self.postorderRec(node.right, list) list.append(node.data); |
Doodle
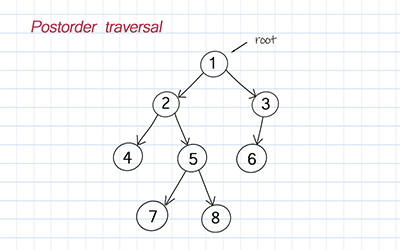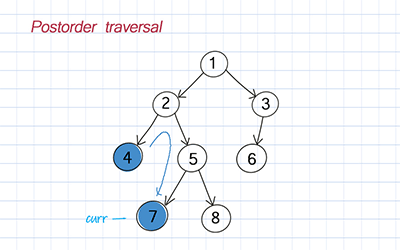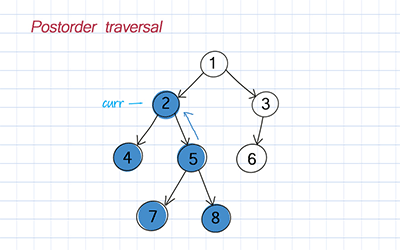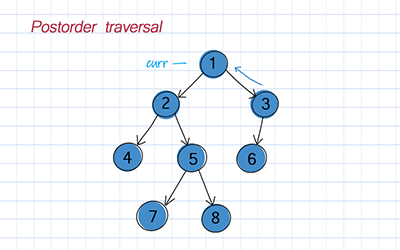
Levelorder traversal
On the other hand, breadth-first search uses levelorder. It is to traverse nodes level by level. The level of a particular node refers to how many generations the node is from the root. We use a queue to implement BFS.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
//Level order traversal, Iteration, Time O(n), Space O(n) public List<T> levelOrder() { if (root == null) return null; List<T> list = new ArrayList<>(); Queue<TreeNode<T>> q = new LinkedList<>(); q.add(root); while (!q.isEmpty()) { TreeNode<T> curr = q.poll(); list.add(curr.data); if(curr != null) { if (curr.left != null) q.add(curr.left); if (curr.right != null) q.add(curr.right); } } return list; } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
//Level order traversal, iteration, Time O(n), Space O(n) levelOrder() { let list = [] if (!this.root) return list let queue = [this.root] while (queue.length > 0) { let curr = queue.pop() list.push(curr.data) if (curr.left) queue.unshift(curr.left) if (curr.right) queue.unshift(curr.right) } return list } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
#Level order traversal, Iteration, Time O(n), Space O(n) def levelOrder(self) : list = [] if self.root is None: return list queue = [self.root] while (len(queue) >0): curr = queue.pop(0) list.append(curr.data) if curr.left is not None: queue.append(curr.left) if curr.right is not None: queue.append(curr.right) return list |
Doodle
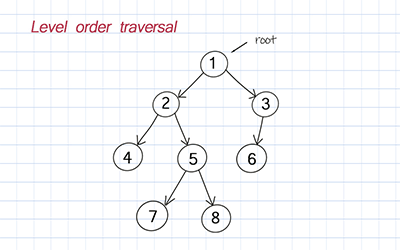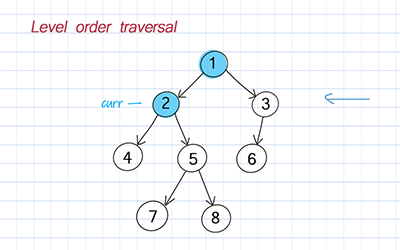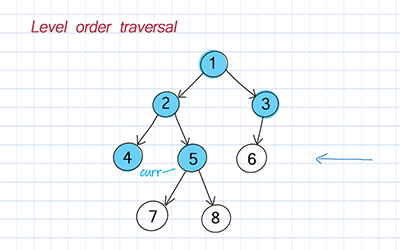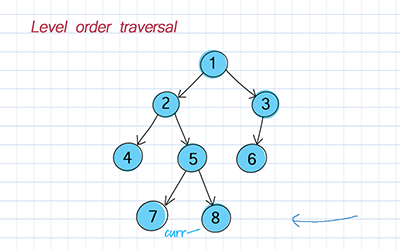
How to implement a binary tree?
First, define a TreeNode class. It has one data attribute and two references to two child nodes. Then you can start to build a binary tree by connecting one node as another node’s child.
Free download
Download binary tree implementation in Java, JavaScript and Python
Data structures illustration PDF