Merge sort uses the divide and conquer technique to provide fast and stable sorting. Divide-and-conquer is a technique that works by recursively breaking down a problem into two or more sub-problems of the same or related type until these become simple enough to be solved directly. This merge sort gif uses animation to demonstrate how merge sort works.
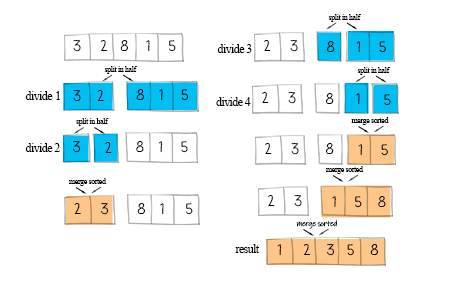
How merge sort works?
It divides the array in half recursively until to single item. Then merges two sorted arrays until all elements are sorted.
What is the time complexity of merge sort?
Merge sort operates in O(nlogn) time. It is faster than simple sorting such as bubble sort, selection sort and insertion sort. The space complexity is O(n) because it uses an extra array when merge.
Merge sort gif
Merge sort Implementation
The merge method is to compare each element in two sorted array one by one, put the smaller one in the third array until one of arrays reaches the end. Then copy the rest of unfinished array to the third array. This requires an additional array in memory, equal in size to the one being sorted.
Merge sort is an efficient sorting technique. It has O(nlogn) complexity. The downside is that it requires extra space for the additional array. The space complexity is O(n).
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
import arrays.Array; public class MergeSort { //Wrapper, Time O(n*logn), Space O(n), n is array length public static void mergeSort(int arr[]) { sortHelper(arr, 0, arr.length-1); } //Helper, recursion, Time O(n*logn), Space O(logn) private static void sortHelper(int[] arr, int low, int high) { if (low >= high) { return; } int mid = low + (high-low)/2; sortHelper(arr, low, mid); sortHelper(arr, mid+1, high); merge(arr, low, high); } //Merge, Time O(n), Space O(n) private static void merge(int[] arr, int low, int high) { int mid = low + (high-low)/2; int i = low; //start of left int j = mid + 1; //start of right int sub[] = new int[high-low+1]; //sub-array int k = 0; //index of sub-array while (i <= mid && j <= high) { if (arr[i] <= arr[j]) sub[k++] = arr[i++]; else sub[k++] = arr[j++]; } while(i <= mid) sub[k++] = arr[i++]; while(j <= high) sub[k++] = arr[j++]; i = low; for(int r = 0; r < sub.length; r++){ arr[i++] = sub[r]; } } public static void main(String[] args) { int[] a = {19, 33, 4 , 61, 5, 38, -36, 21, 0}; System.out.print("Input: "); Array.print(a); mergeSort(a); System.out.print("Merge sort: "); Array.print(a); } } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
//Recursion, Time O(n*logn), Space O(n), n is array length function mergeSort(arr) { if (arr.length < 2) return arr var mid = arr.length / 2 var left = arr.slice(0, mid) var right = arr.slice(mid, arr.length) var sortedLeft = mergeSort(left) var sortedRight = mergeSort(right) return merge(sortedLeft, sortedRight) } //Merge, Time O(n), Space O(n) function merge(left, right) { var arr = [] while (left.length && right.length) { if (left[0] < right[0]) { arr.push(left.shift()) } else { arr.push(right.shift()) } } while (left.length) { arr.push(left.shift()) } while (right.length) { arr.push(right.shift()) } return arr } a = [19, 33, 4 , 61, 5, 38, -36, 21, 0] b = mergeSort(a); console.log("Merge sort: " + b); |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# Recursion, Time O(n*logn), Space O(n), n is array length def mergeSort(arr): if len(arr) < 2: return mid = len(arr) // 2 left = arr[:mid] right = arr[mid:] # Recursive call on each half mergeSort(left) mergeSort(right) #merge two i = 0 j = 0 k = 0 while i < len(left) and j < len(right): if left[i] <= right[j]: arr[k] = left[i] i += 1 else: arr[k] = right[j] j += 1 k += 1 #remaining while i < len(left): arr[k] = left[i] i += 1 k += 1 while j < len(right): arr[k]=right[j] j += 1 k += 1 return arr array = [19, 33, 4 , 61, 5, 38, -36, 21, 0] mergeSort(array) print(array) |
Download
Download merge sort Java, JavaScript and Python code
Sorting doodles compilation (YouTube)
