A disjoint set is a forest data structure, in which there might be multiple trees. A disjoint set contains a set of elements that can be partitioned into subsets. A subset is one tree. There is one element at the root position which is representative of this subset. Other elements are children of this root. So one subset can be seen as a nary tree. Multiple subsets form a disjoint set.
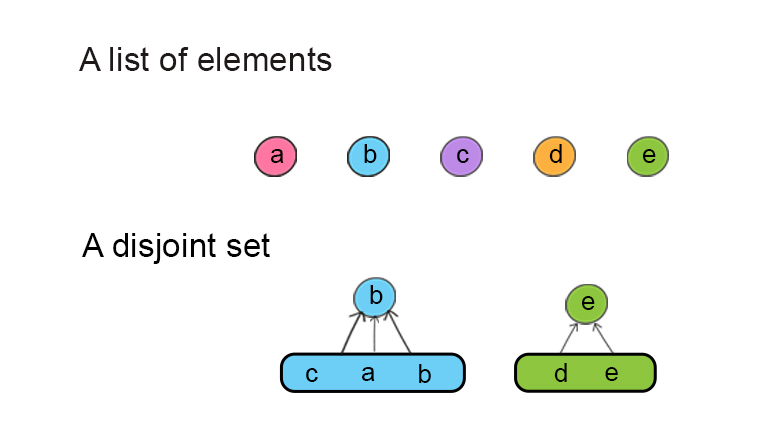
A disjoint set uses union and find methods to construct. So the data structure is also called union-find. Multiple subsets can be merged into a bigger subset when you call a union method to link two elements in two subsets. A find method is used to find the root of the subset.
A disjoint set is usually used as an alternative solution for graph problems, such as finding suggested friends in social media or a minimum spanning tree of a graph.
Table of Content
Build a disjoint set
A disjoint set consists of elements. Each element has a value and a parent pointer to its parent element. An element is also associated with a rank, which identifies the element’s position in a set. So in a DisjointSet class, there are two attributes, parent and rank. Both are maps, in which the keys are elements. From the element, you can find its parent and rank.
makeSet() is a method to initialize parent and rank from a list of elements. Initially, each element can be seen as a subset. Its parent is itself as well. All element’s rank is zero.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import java.util.*; public class DisjointSet<T> { private Map<T, T> parent = new HashMap<>(); private Map<T, Integer> rank = new HashMap<>(); //Create disjoint sets from the list, // Time O(n), Space O(n), n is length of the list public void makeSet(List<T> list) { for (T x : list) { parent.put(x, x); rank.put(x, 0); } } |
JavaScript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
class DisjointSet { // Constructor, Time O(1), Space O(1) constructor() { this.rank = new Map(); this.parent = new Map(); } //Create disjoint sets from the list, // Time O(n), Space O(n), n is length of the list makeSet(list) { for (let x of list) { this.parent.set(x, x); this.rank.set(x, 0) } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 |
class DisjointSet: #Constructor, Time O(1), Space O(1) def __init__(self) : self.parent = {} self.rank = {} # Create disjoint sets from the list, # Time O(n), Space O(n), n is length of the list def make_set(self, list): for x in list: self.parent[x] = x self.rank[x] = 0 |
Find
The find method is to find the element’s root. It follows the chain of parent pointers up the tree until it reaches the root. Save this root as the value in parent. Multiple elements can share the same root. This root element is the representative member of the set to which elements belong.
How does path compression work in a disjoint set?
Path compression is a technique that uses recursions to flatten the structure of the tree by making the element’s parent point to the root. The root is also part of the set. The flattened tree reduces the step to find an element to its root. The time complexity is O(α(n)), where α(n) is the extremely slow-growing inverse Ackermann function. This is better than O(logn). The space complexity is O(α(n)) as well because it uses recursion for the function’s call stack.
Java
|
1 2 3 4 5 6 7 8 |
// Recursion, Find the root of the set in which x belongs // Time O(α(n)), Space O(α(n)), α(n) is the inverse ackermann function public T find(T x){ if (parent.get(x) != x) { parent.put(x, find(parent.get(x))); // path compression } return parent.get(x); } |
JavaScript
|
1 2 3 4 5 6 7 8 |
// Recursion, Find the root of the set in which x belongs // Time O(α(n)), Space O(α(n)), α(n) is the inverse ackermann function find(x) { if (this.parent.get(x) !== x) { this.parent.set(x, this.find(this.parent.get(x))); // path compression } return this.parent.get(x); } |
Python
|
1 2 3 4 5 6 |
# Recursion, Find the root of the set in which x belongs # Time O(α(n)), Space O(α(n)), α(n) is the inverse ackermann function def find(self, x): if self.parent[x] != x: self.parent[x] = self.find(self.parent[x]) # path compression return self.parent[x] |
Union
The union method is to make two elements into the same set. It uses the find() method to find the roots of both elements. If they belong to different sets, the sets are combined by attaching one root to the other one as a child.
How union by rank works in a disjoint set?
Union by rank is a technique to keep the height of the tree as small as possible. Union by rank attaches the shorter tree to the root of the taller tree. The element’s rank is 0 initially. If two sets are combined and have the same rank, the resulting set’s rank increases by 1. If two sets have different ranks, the resulting set’s rank is the larger one of the two. The time complexity and space complexity is O(α(n)).
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
// Union of two subsets, Time O(α(n)), Space O(α(n)) public void union(T a, T b) { T x = find(a); //find the root of the sets of a and b T y = find(b); if (x == y) // if x and y are present in same set return; if (rank.get(x) > rank.get(y)) //union by rank parent.put(y, x); else if (rank.get(x) < rank.get(y)) parent.put(x, y); else { parent.put(x, y); rank.put(y, rank.get(y) + 1); } } |
JavaScript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
// Union of two subsets, Time O(α(n)), Space O(α(n)) union(a, b) { let x = this.find(a); //find the root of the sets of a and b let y = this.find(b); if (x == y) return; // if x and y are present in same set if (this.rank.get(x) < this.rank.get(y)) { //union by rank this.parent.set(x, y); } else if (this.rank.get(x) > this.rank.get(y)) { this.parent.set(y, x); } else { this.parent.set(x, y); this.rank.set(y, this.rank.get(y) + 1); } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# Union of two subsets, Time O(α(n)), Space O(α(n)) def union(self, a, b): x = self.find(a) # find the root of the sets of a and b y = self.find(b) if x == y: # if x and y in the same set return if self.rank[x] > self.rank[y]: # union by rank self.parent[y] = x elif self.rank[x] < self.rank[y]: self.parent[x] = y else: self.parent[x] = y self.rank[y] = self.rank[y] + 1 |
Print
Print is a utility method to print out elements in each subset. Each subset has a root (or parent) and all elements in this set. So the disjoint set is printed out like a hash map.
Java
|
1 2 3 4 5 6 7 8 9 10 11 |
// print the sets as hashmap, key is root, value is elements in a set. // Time O(nxα(n)), Space O(nxα(n)) public void printSets(List<T> list){ Map<T, Set<T>> res= new HashMap<>(); for (T i : list) { T p = find(i); res.putIfAbsent(p, new HashSet<T>()); res.get(p).add(i); } System.out.println(res); } |
JavaScript
|
1 2 3 4 5 6 7 8 9 10 11 12 |
// print the sets as hashmap, key is root, value is elements in a set. // Time O(nxα(n)), Space O(nxα(n)) printSets(list){ let res = new Map(); for(let i of list) { let p = this.find(i) if (res.get(p) == null) res.set(p, new Set()) res.get(p).add(i); } console.log(res) } |
Python
|
1 2 3 4 5 6 7 8 9 10 |
# print the sets as hashmap, key is root, value is elements in a set. # Time O(nxα(n)), Space O(nxα(n)) def print_sets(self, list): res = {} for x in list : p = self.find(x) # parent node if p not in res: res[p] = set() res[p].add(x); print(res) |
Free download
Download Disjoint set/Union find in Java, JavaScript and Python
Data structures and Java collections